Capítulo 25 Comparação de mais de dois grupos

Assim como na comparação entre dois grupos, ao desejarmos comparar mais de dois grupos em uma análise estatística, é fundamental selecionar o teste mais adequado de acordo com as características dos dados. Os testes podem ser paramétricos ou não paramétricos, e a escolha correta depende da verificação prévia de alguns pressupostos, como normalidade, homogeneidade de variâncias e independência das observações.

25.1 Revisando as hipóteses da comparação entre dois grupos

Paramétrico (Teste t)
- Não pareado (t de Student):
  - H₀: As médias dos dois grupos são iguais (μ₁ = μ₂)
  - H₁: As médias dos dois grupos são diferentes (μ₁ ≠ μ₂)
- Pareado (t pareado):
  - H₀: A média das diferenças entre os pares é igual a zero (μ_d = 0)
  - H₁: A média das diferenças entre os pares é diferente de zero (μ_d ≠ 0)
Não paramétrico
- Não pareado (Mann-Whitney/Wilcoxon rank-sum):
  - H₀: As distribuições dos dois grupos são iguais
  - H₁: As distribuições dos dois grupos são diferentes
- Pareado (Wilcoxon signed-rank):
  - H₀: A distribuição das diferenças entre os pares é simétrica em torno de zero
  - H₁: A distribuição das diferenças entre os pares não é simétrica em torno de zero

Na comparação entre dois grupos, tanto nos testes paramétricos quanto nos não paramétricos, a hipótese nula (H₀) geralmente afirma que as médias (ou distribuições) dos dois grupos são iguais, enquanto a hipótese alternativa (H₁) aponta que elas são diferentes. Ou seja, o teste busca identificar uma diferença específica entre os dois grupos analisados.

25.2 Hipóteses para a comparação entre mais de dois grupos

Paramétrico (ANOVA)
- Não pareado (ANOVA one-way):
  - H₀: As médias dos grupos são todas iguais (μ₁ = μ₂ = … = μ_k)
  - H₁: Pelo menos uma média de grupo é diferente das outras
- Pareado (ANOVA de medidas repetidas):
  - H₀: As médias dos tratamentos (ou condições) são iguais
  - H₁: Pelo menos uma média de tratamento é diferente das outras
Não paramétrico
- Não pareado (Kruskal-Wallis):
  - H₀: As distribuições dos grupos são todas iguais
  - H₁: Pelo menos uma distribuição de grupo é diferente das outras
- Pareado (Friedman):
  - H₀: As distribuições dos tratamentos (ou condições) são todas iguais
  - H₁: Pelo menos uma distribuição de tratamento é diferente das outras

Na comparação entre mais de dois grupos (por exemplo, usando ANOVA ou Kruskal-Wallis), a hipótese nula (H₀) é que todas as médias (ou distribuições) dos grupos são iguais. Por outro lado, a hipótese alternativa (H₁) não especifica qual grupo é diferente, mas sim que pelo menos um dos grupos se difere dos demais. Ou seja, a rejeição da hipótese nula indica que existe pelo menos uma diferença, mas não revela imediatamente entre quais grupos essa diferença ocorre.

Atenção: É importante notar que, no contexto de mais de dois grupos, a hipótese alternativa não identifica quais grupos são diferentes, apenas aponta que existe pelo menos uma diferença.

25.3 Testes Paramétricos

Não Pareados: O teste mais utilizado é a ANOVA de uma via, que compara as médias de três ou mais grupos independentes.
Pareados: Utiliza-se a ANOVA para medidas repetidas quando as medições são feitas nos mesmos indivíduos em diferentes condições ou tempos.

25.3.1 Pré-requisitos para ANOVA (dados pareados ou não)

Normalidade dos resíduos: Os resíduos do modelo devem seguir uma distribuição normal.
Homogeneidade de variâncias: As variâncias dos grupos devem ser semelhantes.
Esfericidade (apenas para medidas repetidas): A variância das diferenças entre todas as combinações de pares de grupos deve ser semelhante.
Independência das observações: Para grupos independentes.

Se algum desses pré-requisitos não for atendido, é recomendado utilizar testes não paramétricos.

25.4 Testes Não Paramétricos

Não Pareados: O teste de Kruskal-Wallis é utilizado para comparar mais de dois grupos independentes.
Pareados: O teste de Friedman é usado para comparar três ou mais grupos pareados.

25.5 ANOVA de uma via no R

A seguir, apresentamos um exemplo de ANOVA de uma via e do teste de Kruskal-Wallis, incluindo a verificação dos pré-requisitos.

25.5.1 Simulação de Dados

set.seed(123)
grupo <- factor(rep(c("A", "B", "C"), each = 10))
valor <- c(rnorm(10, mean = 5, sd = 1),
           rnorm(10, mean = 6, sd = 1),
           rnorm(10, mean = 7, sd = 1))
dados <- data.frame(grupo, valor)

25.5.2 Visualização dos Dados

boxplot(valor ~ grupo, data = dados, main = "Boxplot dos Grupos", ylab = "Valor")

25.5.3 Verificação dos Pré-requisitos para ANOVA

25.5.3.1 Normalidade dos resíduos

modelo_aov <- aov(valor ~ grupo, data = dados)
residuos <- residuals(modelo_aov)

shapiro.test(residuos)

## 
##  Shapiro-Wilk normality test
## 
## data:  residuos
## W = 0.96213, p-value = 0.3507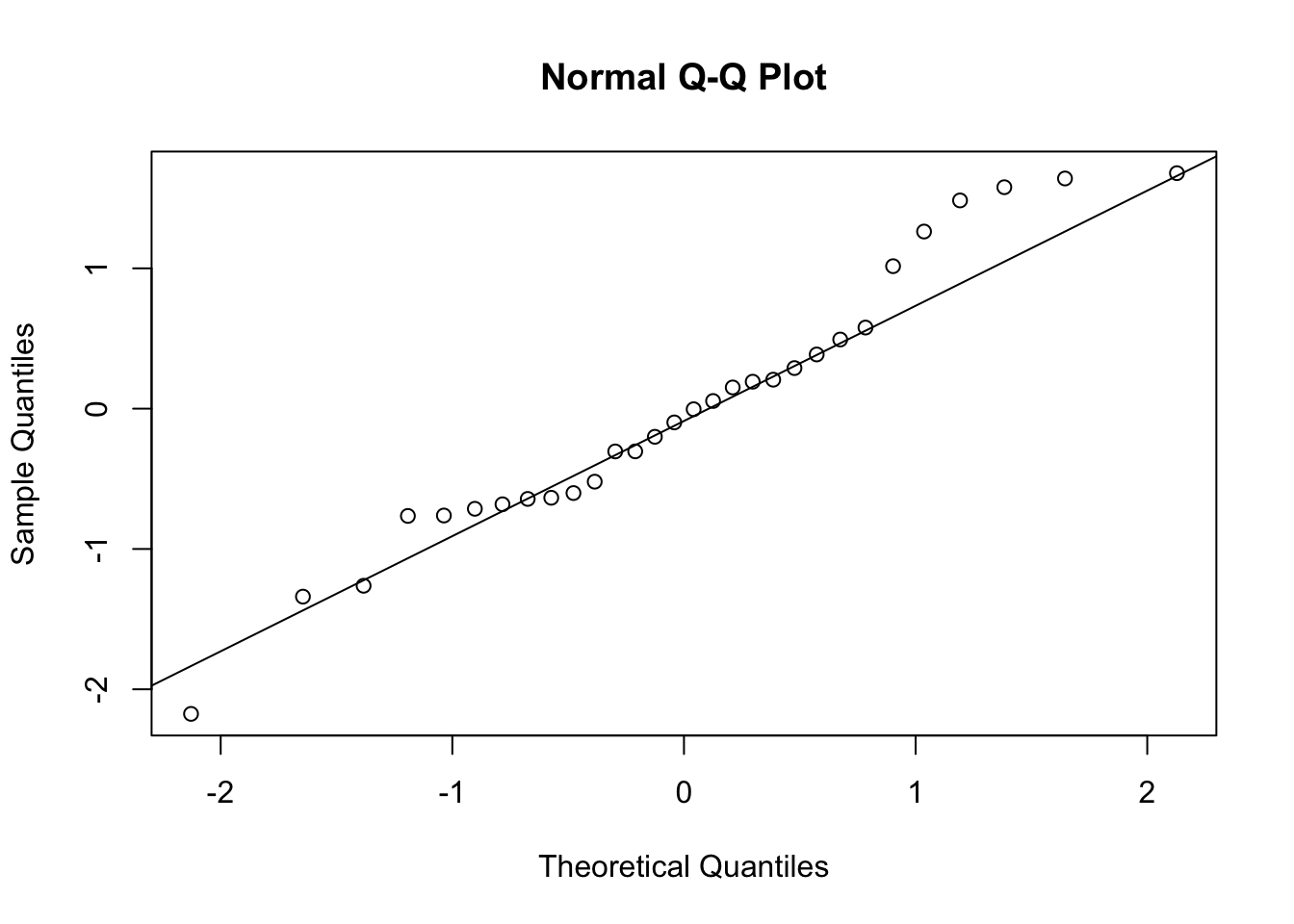

qqnorm(residuos)
qqline(residuos)

A função aov no R é utilizada para realizar análise de variância (ANOVA).
modelo_aov <- aov(valor ~ grupo, data = dados)
Esta linha ajusta um modelo de ANOVA de uma via, avaliando se a média da variável valor difere entre os diferentes níveis do fator grupo, usando os dados do data frame dados.
residuos <- residuals(modelo_aov)
Esta linha extrai os resíduos do modelo ajustado, ou seja, as diferenças entre os valores observados e os valores previstos pelo modelo. A análise dos resíduos é fundamental para verificar os pressupostos da ANOVA, como a normalidade.

Neste exemplo, tanto o teste de normalidade quanto a inspeção visual do gráfico QQ sugerem que os resíduos seguem uma distribuição normal.

25.5.3.2 Homogeneidade de variâncias

# Instale 'car' se necessário: install.packages("car")
library(car)
leveneTest(valor ~ grupo, data = dados)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2   5e-04 0.9995
##       27

O teste de Levene avalia a homogeneidade das variâncias entre os grupos, que é um dos pré-requisitos para a ANOVA.
Valor de p (Pr(>F)) = 0.9995: O valor de p é muito maior que 0,05, indicando que não há evidências para rejeitar a hipótese nula de igualdade das variâncias.

Nesse exemplo, as variâncias dos grupos podem ser consideradas homogêneas. Portanto, o pré-requisito de homogeneidade de variâncias para a ANOVA foi atendido.

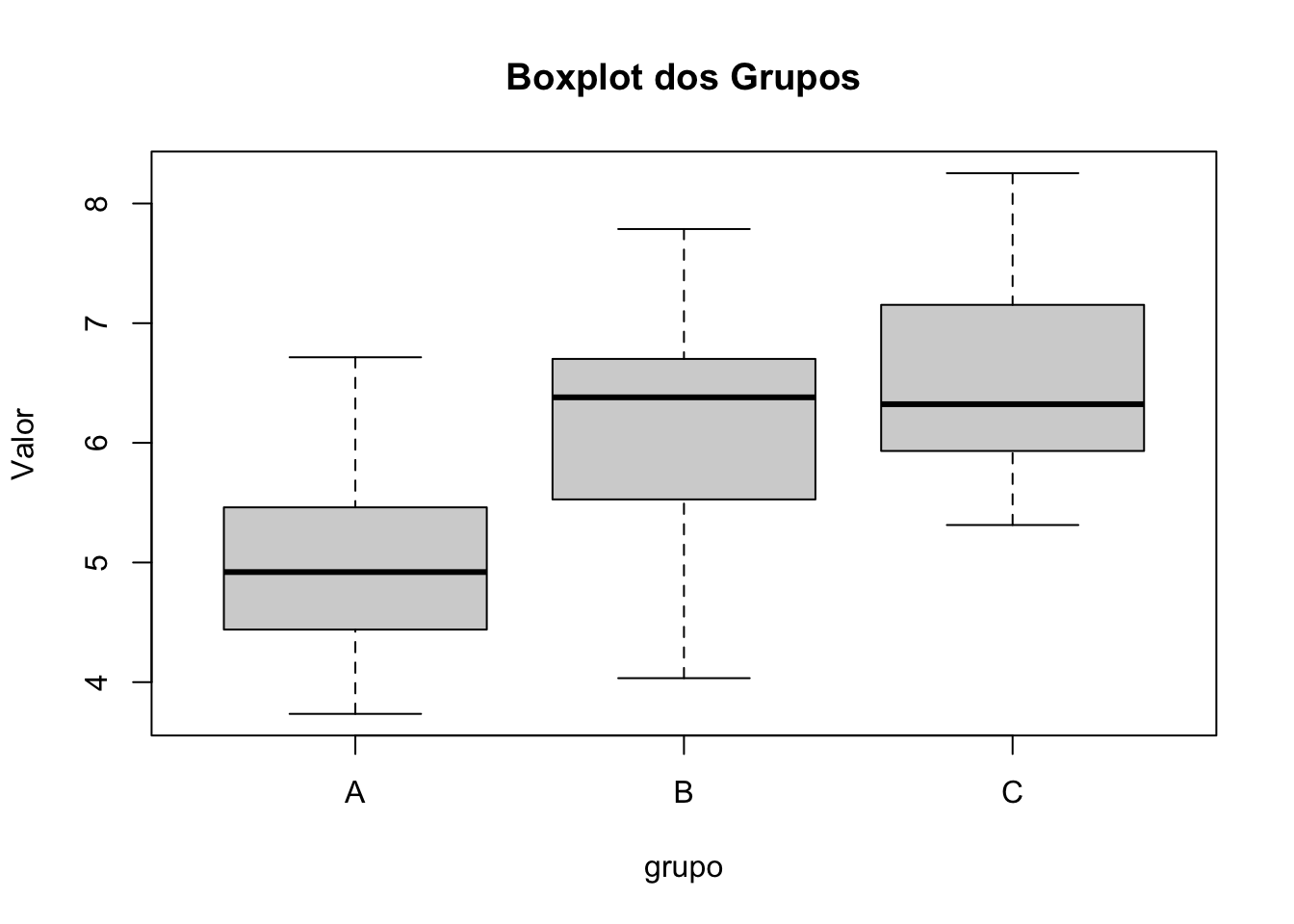
25.5.4 ANOVA de Uma Via

summary(modelo_aov)

##             Df Sum Sq Mean Sq F value  Pr(>F)   
## grupo        2  12.24   6.122   6.435 0.00518 **
## Residuals   27  25.68   0.951                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Valor de p (Pr(>F)) = 0.00518: O valor de p é menor que 0,05, indicando que existem diferenças estatisticamente significativas entre as médias dos grupos analisados.
Rejeita-se a hipótese nula de igualdade das médias. Isso significa que pelo menos um dos grupos difere significativamente dos demais. Recomenda-se realizar testes post hoc (por exemplo, Tukey) para identificar quais grupos apresentam diferenças entre si.

25.5.4.1 Teste Post Hoc (se ANOVA for significativa)

TukeyHSD(modelo_aov)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = valor ~ grupo, data = dados)
## 
## $grupo
##          diff         lwr      upr     p adj
## B-A 1.1339963  0.05254072 2.215452 0.0384525
## C-A 1.5008155  0.41935988 2.582271 0.0052283
## C-B 0.3668192 -0.71463643 1.448275 0.6812485

O teste de Tukey compara as médias dos grupos dois a dois, após a ANOVA indicar diferença significativa entre eles. Os resultados mostram as diferenças entre as médias dos grupos (diff), os limites inferior (lwr) e superior (upr) do intervalo de confiança de 95%, e o valor de p ajustado (p adj).

Resultados:

B vs A:
Diferença = 1.13; IC 95% = [0.05, 2.22]; p = 0.038
→ O grupo B tem média significativamente maior que o grupo A.
C vs A:
Diferença = 1.50; IC 95% = [0.42, 2.58]; p = 0.005
→ O grupo C tem média significativamente maior que o grupo A.
C vs B:
Diferença = 0.37; IC 95% = [-0.71, 1.45]; p = 0.681
→ Não há diferença significativa entre os grupos C e B.

Os grupos B e C apresentam médias significativamente maiores do que o grupo A. Não foi observada diferença significativa entre os grupos B e C.

25.6 Kruskal-Wallis no R

Se os pré-requisitos da ANOVA não forem atendidos, utilize o Kruskal-Wallis:

kruskal.test(valor ~ grupo, data = dados)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  valor by grupo
## Kruskal-Wallis chi-squared = 8.1858, df = 2, p-value = 0.01669

Valor de p (p-value) = 0.01669: O valor de p é menor que 0,05, indicando que há diferença estatisticamente significativa entre pelo menos dois dos grupos analisados.
Rejeita-se a hipótese nula de que as distribuições dos grupos são todas iguais. Ou seja, pelo menos um dos grupos apresenta distribuição diferente dos demais. Para identificar especificamente quais grupos diferem entre si, é recomendada a realização de testes post hoc apropriados (por exemplo, Dunn ou pairwise Wilcoxon com ajuste para múltiplas comparações).

25.6.1 Teste Post Hoc para Kruskal-Wallis

# Instale PMCMRplus se necessário: install.packages("PMCMRplus")
library(PMCMRplus)
kwAllPairsDunnTest(valor ~ grupo, data = dados)

##   A     B    
## B 0.058 -    
## C 0.021 0.611

O teste de Dunn é um teste pós-hoc não-paramétrico, utilizado após o teste de Kruskal-Wallis para identificar quais pares de grupos diferem significativamente entre si.

Os p-valores apresentados pelo teste compara todos os pares possíveis entre os grupos (neste exemplo: A, B e C):

A vs. B: p = 0.058
A vs. C: p = 0.021
B vs. C: p = 0.611

Portanto, os resultados sugerem que apenas os grupos A e C, para a variável analisada, são estatisticamente diferentes entre si.

25.7 Por que não é indicado comparar os grupos dois a dois diretamente?

Quando se tem mais de dois grupos, pode parecer tentador realizar múltiplos testes de comparação entre pares de grupos (por exemplo, vários testes t para todos os pares possíveis). No entanto, esse procedimento não é recomendado, pois aumenta significativamente o risco de cometer um erro do tipo I (falso positivo).

Cada teste realizado tem uma determinada probabilidade de indicar uma diferença por acaso (erro tipo I), geralmente 5% se α = 0,05. Ao fazer muitos testes independentes, a probabilidade de encontrar pelo menos um resultado “significativo” apenas por acaso aumenta. Esse fenômeno é chamado de inflacionamento da taxa de erro tipo I.

Por isso, para comparação de mais de dois grupos, utiliza-se primeiro um teste global (como ANOVA ou Kruskal-Wallis). Se o resultado for significativo, aí sim são realizados testes post hoc, que já incluem correções para múltiplas comparações (como o teste de Tukey), controlando o risco de erro tipo I.

25.8 ANOVA para Dados Repetidos no R

Vamos analisar o desempenho de 6 alunos em 3 provas diferentes (Prova 1, Prova 2 e Prova 3). Cada aluno fez todas as provas, ou seja, temos medidas repetidas!

25.8.1 Gerar dados simulados

set.seed(123)
n <- 20
dados <- data.frame(
  aluno = factor(1:n),
  prova1 = round(rnorm(n, mean = 7, sd = 1), 1),
  prova2 = round(rnorm(n, mean = 7.5, sd = 1), 1),
  prova3 = round(rnorm(n, mean = 8, sd = 1), 1)
)
head(dados)

##   aluno prova1 prova2 prova3
## 1     1    6.4    6.4    7.3
## 2     2    6.8    7.3    7.8
## 3     3    8.6    6.5    6.7
## 4     4    7.1    6.8   10.2
## 5     5    7.1    6.9    9.2
## 6     6    8.7    5.8    6.9

25.8.2 Converter para formato longo

library(tidyr)
dados_long <- pivot_longer(
  dados,
  cols = c("prova1", "prova2", "prova3"),
  names_to = "prova",
  values_to = "nota"
)
head(dados_long)

## # A tibble: 6 × 3
##   aluno prova   nota
##   <fct> <chr>  <dbl>
## 1 1     prova1   6.4
## 2 1     prova2   6.4
## 3 1     prova3   7.3
## 4 2     prova1   6.8
## 5 2     prova2   7.3
## 6 2     prova3   7.8

Transformar os dados para o formato longo é fundamental para análises de medidas repetidas porque permite que o R identifique corretamente as repetições de cada aluno ao longo das diferentes provas. Sem isso, não é possível fazer ANOVA de medidas repetidas de forma adequada!

25.8.3 Visualização (opcional)

library(ggplot2)
library(RColorBrewer)

# Use uma paleta de cores apropriada para até 20 alunos
cores <- colorRampPalette(brewer.pal(9, "Set1"))(20)

ggplot(dados_long, aes(x = prova, y = nota, group = aluno, color = aluno)) +
  geom_line(alpha = 0.7, size = 1) +
  geom_point(size = 2) +
  labs(x = "Avaliações", y = "Pontuação") +
  scale_color_manual(values = cores) +
  labs(title = "Notas dos Alunos nas Três Provas", color = "Aluno") +
  theme_minimal() +
  theme(legend.position = "right")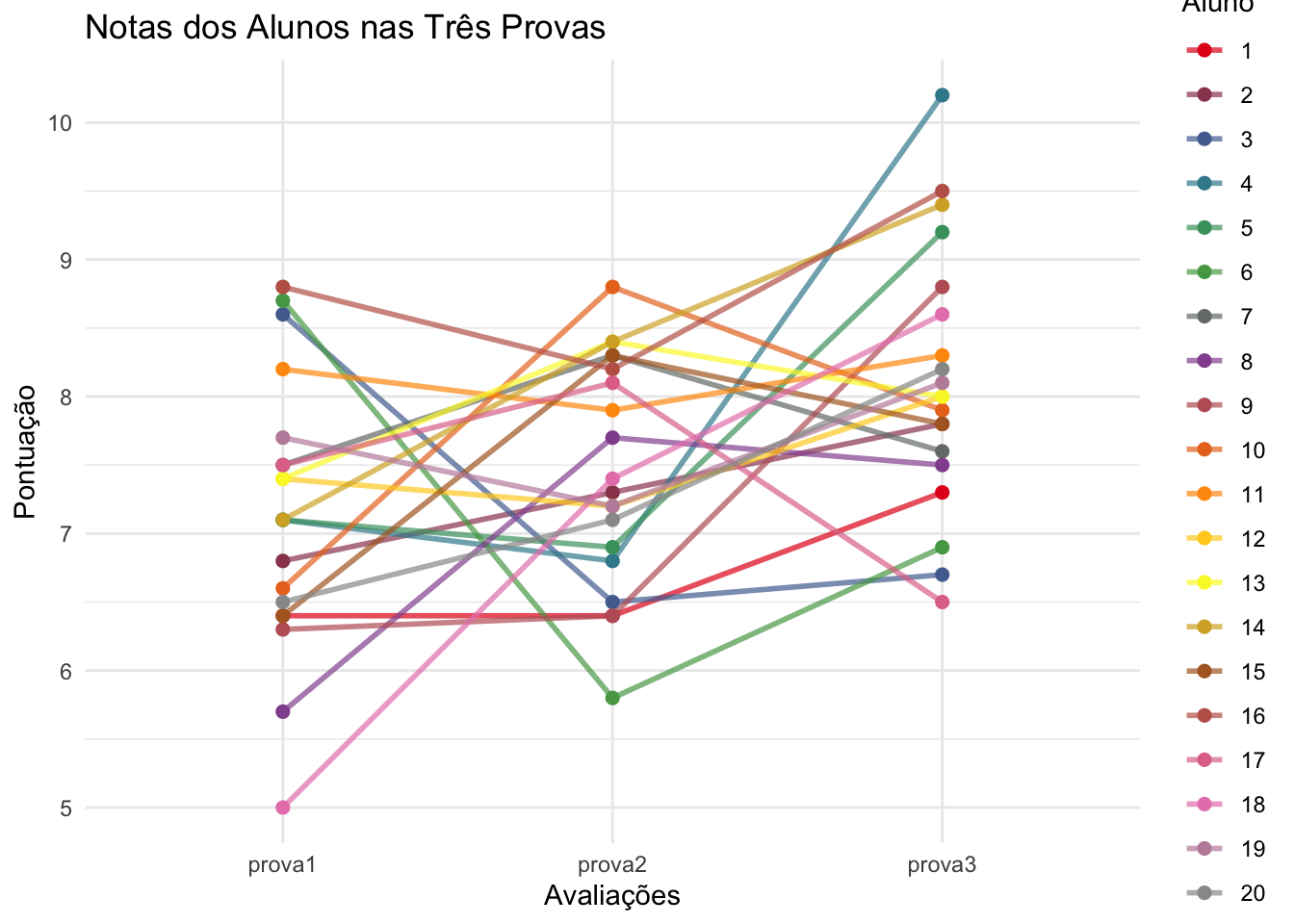

25.8.4 Teste de normalidade das diferenças (pré-requisito)

dif12 <- dados$prova1 - dados$prova2
dif13 <- dados$prova1 - dados$prova3
dif23 <- dados$prova2 - dados$prova3

qqnorm(dif12)
qqline(dif12)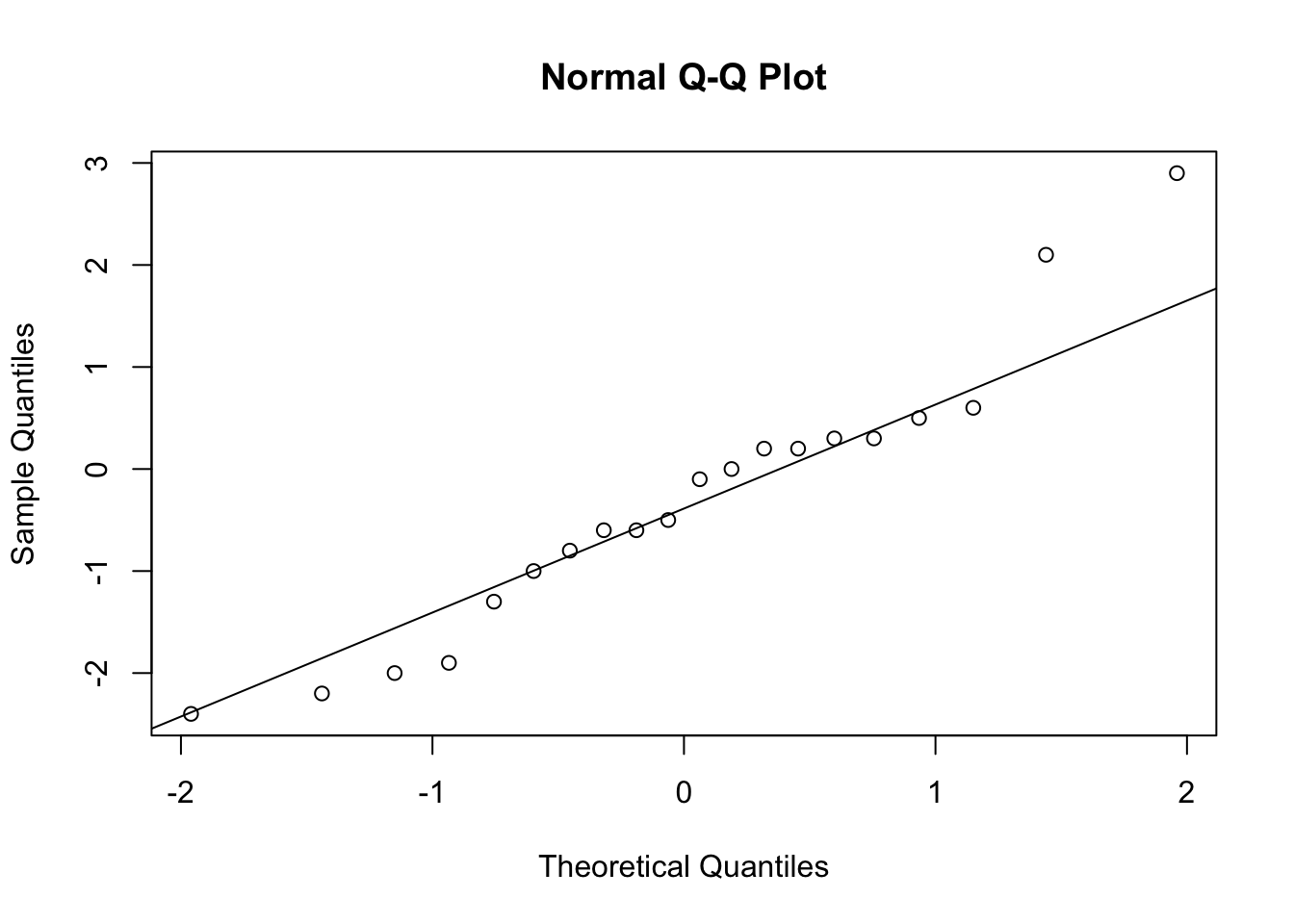

shapiro.test(dif12)

## 
##  Shapiro-Wilk normality test
## 
## data:  dif12
## W = 0.94596, p-value = 0.3099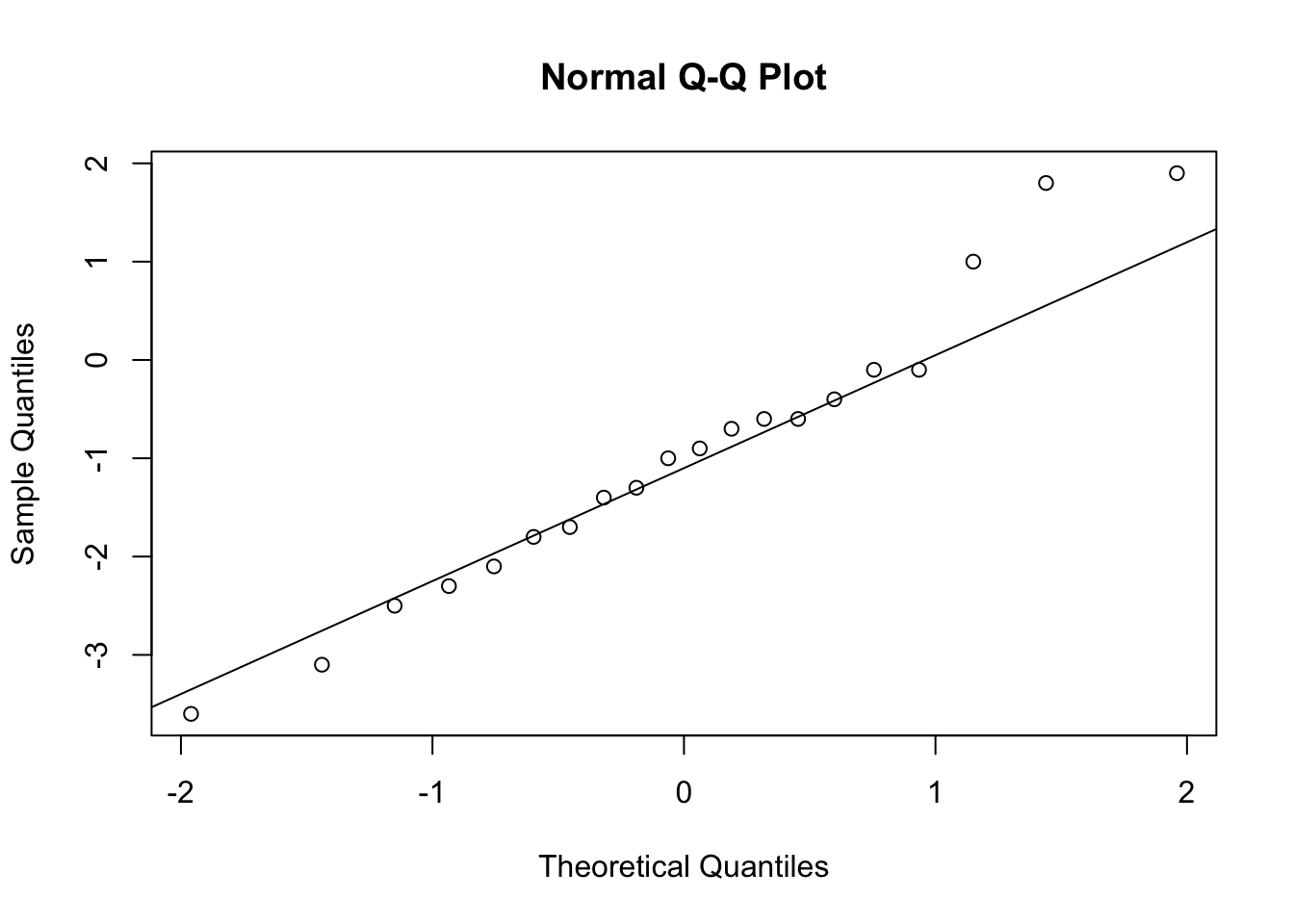

qqnorm(dif13)
qqline(dif13)

shapiro.test(dif13)

## 
##  Shapiro-Wilk normality test
## 
## data:  dif13
## W = 0.96929, p-value = 0.7398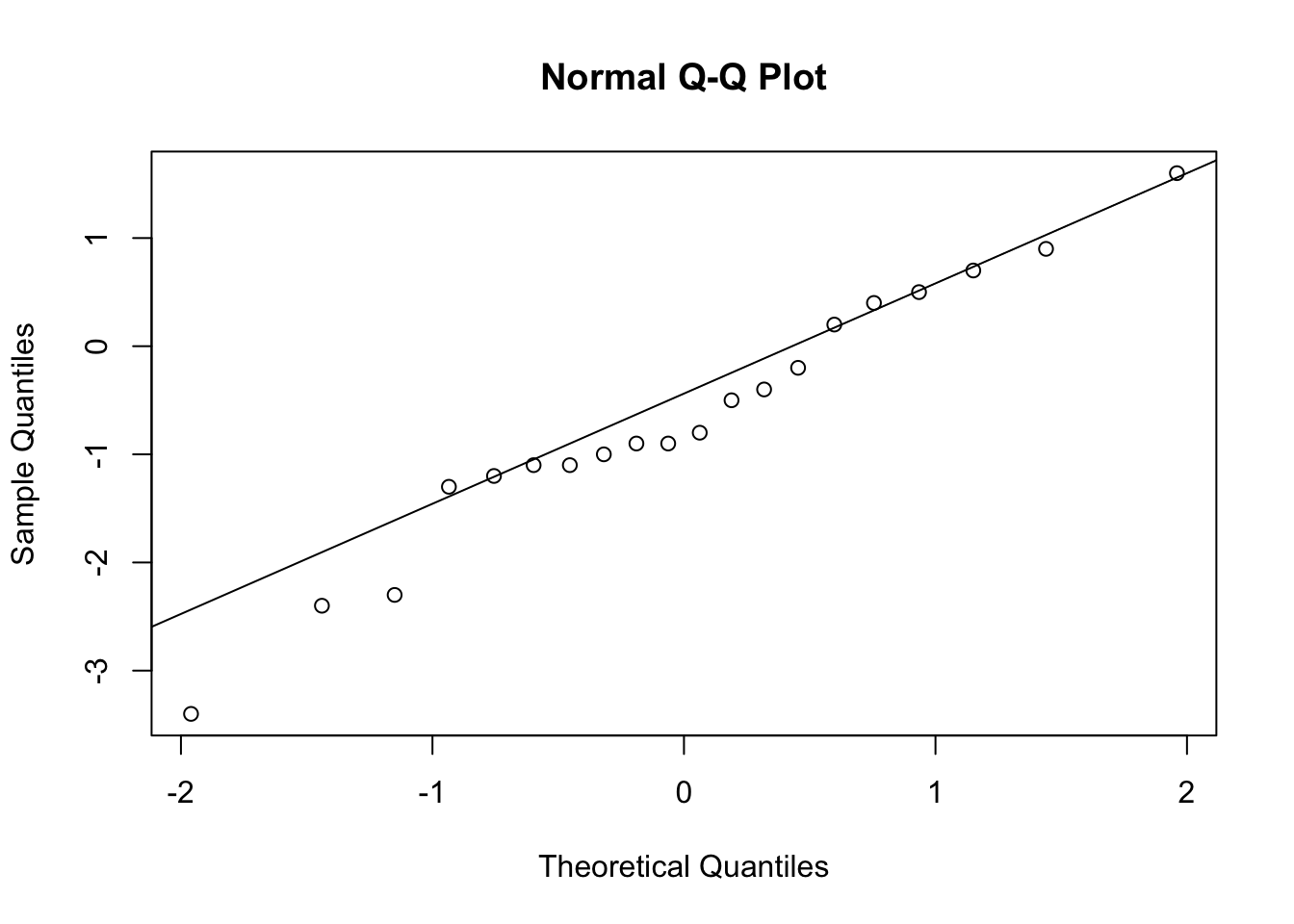

qqnorm(dif23)
qqline(dif23)

shapiro.test(dif23)

## 
##  Shapiro-Wilk normality test
## 
## data:  dif23
## W = 0.97175, p-value = 0.7914

As diferenças seguem distribuição normal.

25.8.5 ANOVA de medidas repetidas com afex (testa e corrige esfericidade)

A função aov_ez(), do pacote afex realiza toda a ANOVA de medidas repetidas de forma prática e automática.

# Instale se necessário: install.packages("afex")
library(afex)
modelo_afex <- aov_ez(
  id = "aluno",
  dv = "nota",
  within = "prova",
  data = dados_long
)
modelo_afex

## Anova Table (Type 3 tests)
## 
## Response: nota
##   Effect          df  MSE       F  ges p.value
## 1  prova 1.91, 36.27 0.94 5.53 ** .168    .009
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
## 
## Sphericity correction method: GG

Effect: O fator analisado (prova), ou seja, se as notas variam entre as provas.
df: Graus de liberdade. Note que aparecem valores decimais (1.91, 36.27) porque foi aplicada a correção de Greenhouse-Geisser (GG), devido à violação da esfericidade.
MSE: Erro quadrático médio.
F: Estatística F da ANOVA.
ges: Generalized Eta Squared, uma medida de tamanho de efeito.
p.value: Valor de p associado ao teste F. Neste caso, p = 0.009 indica que há diferença significativa entre as médias das provas (p < 0.05).
Observação sobre esfericidade: A linha Sphericity correction method: GG informa que o pressuposto de esfericidade foi violado (teste de Mauchly p < 0.05) e, por isso, os graus de liberdade e o valor de p foram corrigidos automaticamente pelo método de Greenhouse-Geisser.

A análise de variância (ANOVA) mostrou que o fator “prova” teve um efeito significativo sobre as notas (F(1.91, 36.27) = 5.53, p = 0.009, ges = 0.168), indicando que as médias das notas diferem entre as provas.

25.8.6 Pós-hoc: Comparações múltiplas entre as provas

# Instale se necessário: install.packages("emmeans")
library(emmeans)
emm <- emmeans(modelo_afex, ~ prova)
pairs(emm, adjust = "bonferroni") # ou "holm", "sidak", etc.

##  contrast        estimate    SE df t.ratio p.value
##  prova1 - prova2   -0.315 0.300 19  -1.050  0.9212
##  prova1 - prova3   -0.975 0.326 19  -2.993  0.0225
##  prova2 - prova3   -0.660 0.269 19  -2.455  0.0717
## 
## P value adjustment: bonferroni method for 3 tests

prova1 vs prova2: Não há diferença significativa (p = 0.9212).
prova1 vs prova3: Diferença significativa (p = 0.0225). As médias dessas provas são estatisticamente diferentes.
prova2 vs prova3: Não há diferença significativa (p = 0.0717).

A análise revelou que existe diferença significativa nas notas entre as provas. Especificamente, a única diferença significativa foi entre as provas 1 e 3, indicando que as médias dessas avaliações diferem estatisticamente. Entre as demais provas, não foram observadas diferenças significativas após o ajuste de Bonferroni.

25.9 Teste de Friedman

# O teste de Friedman compara as três provas considerando a repetição por aluno
friedman.test(as.matrix(dados[, c("prova1", "prova2", "prova3")]))

## 
##  Friedman rank sum test
## 
## data:  as.matrix(dados[, c("prova1", "prova2", "prova3")])
## Friedman chi-squared = 10.101, df = 2, p-value = 0.006405

25.9.1 Pós-teste: Comparações Múltiplas (Wilcoxon pareado)

pairwise.wilcox.test(
  dados_long$nota,
  dados_long$prova,
  paired = TRUE,
  p.adjust.method = "bonferroni"
)

## 
##  Pairwise comparisons using Wilcoxon signed rank test with continuity correction 
## 
## data:  dados_long$nota and dados_long$prova 
## 
##        prova1 prova2
## prova2 0.729  -     
## prova3 0.033  0.087 
## 
## P value adjustment method: bonferroni

Após o teste de Friedman indicar que há diferença nas notas das provas, fazemos um pós-teste para descobrir entre quais provas há diferença.

Apenas entre Prova 1 e Prova 3 existe diferença significativa (0.033 < 0.05).
Entre Prova 1 e 2, e entre Prova 2 e 3, não há diferença significativa (valores maiores que 0.05).