Capítulo 23 Pacotes pwr, rstatix e effsize

Nesse capítulo, abordaremos como calcular tamanho de amostra, poder estatístico e tamanho do efeito em diferentes testes estatísticos usando os pacotes pwr, rstatix e effsize. O foco será nos testes t (pareado e não pareado) e Wilcoxon (pareado e não pareado), com exemplos práticos e orientações sobre interpretação dos resultados.

Importante: Antes de começar, certifique-se de instalar o pacote pwr, rstatix e effsize:

install.packages(c("pwr", "rstatix", "effsize"))

23.1 Cálculos de tamanho de amostra, poder e efeito com o pacote pwr

O pacote pwr permite calcular:

  • Tamanho de amostra necessário para detectar um determinado efeito;
  • Poder estatístico de um teste para amostras de tamanho fixo;
  • Menor tamanho de efeito que pode ser detectado para um dado poder e amostra.

23.1.1 Exercício 1: Tamanho da amostra para teste t não pareado

Calcule o tamanho da amostra necessário para detectar um efeito moderado (d = 0.5), com poder de 0.8 e nível de significância de 0.05, em um teste t bilateral para duas amostras independentes.

library(pwr)
# Tamanho da amostra para teste t não pareado
pwr.t.test(d = 0.5, power = 0.8, sig.level = 0.05, type = "two.sample")
## 
##      Two-sample t test power calculation 
## 
##               n = 63.76561
##               d = 0.5
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

23.1.2 Exercício 2: Poder do teste t não pareado para n fixo

Se você dispõe de 26 observações em cada grupo, qual é o poder do teste para detectar um efeito de 0.5, com sig.level = 0.05?

# Poder do teste t não pareado para n = 26 por grupo
pwr.t.test(n = 26, d = 0.5, sig.level = 0.05, type = "two.sample")
## 
##      Two-sample t test power calculation 
## 
##               n = 26
##               d = 0.5
##       sig.level = 0.05
##           power = 0.4240344
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

23.1.3 Exercício 3: Menor efeito detectável no teste t não pareado

Com 26 observações por grupo, poder de 0.8 e sig.level de 0.05, qual o menor tamanho de efeito detectável?

# Tamanho do efeito detectável
pwr.t.test(n = 26, power = 0.8, sig.level = 0.05, type = "two.sample")
## 
##      Two-sample t test power calculation 
## 
##               n = 26
##               d = 0.7923522
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

23.1.4 Exercício 4: Repita para outros testes

23.1.4.1 a) Teste t pareado

# Tamanho da amostra para teste t pareado
pwr.t.test(d = 0.5, power = 0.8, sig.level = 0.05, type = "paired")
## 
##      Paired t test power calculation 
## 
##               n = 33.36713
##               d = 0.5
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number of *pairs*
# Poder para n = 26 pares
pwr.t.test(n = 26, d = 0.5, sig.level = 0.05, type = "paired")
## 
##      Paired t test power calculation 
## 
##               n = 26
##               d = 0.5
##       sig.level = 0.05
##           power = 0.6881801
##     alternative = two.sided
## 
## NOTE: n is number of *pairs*
# Tamanho do efeito detectável
pwr.t.test(n = 26, power = 0.8, sig.level = 0.05, type = "paired")
## 
##      Paired t test power calculation 
## 
##               n = 26
##               d = 0.5717051
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number of *pairs*

23.1.4.2 b) Wilcoxon não pareado

# Tamanho da amostra para Wilcoxon não pareado (aproximação pelo teste t)
pwr.t.test(d = 0.5, power = 0.8, sig.level = 0.05, type = "two.sample")
## 
##      Two-sample t test power calculation 
## 
##               n = 63.76561
##               d = 0.5
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Dica: O pacote pwr não possui funções específicas para testes não-paramétricos como Wilcoxon. Por isso, costuma-se usar o cálculo para teste t como aproximação, aumentando o tamanho da amostra em cerca de 15% (multiplique o valor obtido por 1,15), já que testes não-paramétricos geralmente requerem amostras maiores para o mesmo poder estatístico.

# Recalculando o tamanho da amostra
63.76561*1.15
## [1] 73.33045

O tamanho do efeito para o teste de Wilcoxon pode ser aproximado por d × 0,86, sendo d o tamanho do efeito de Cohen, desde que as distribuições dos grupos sejam aproximadamente normais e com variâncias semelhantes (Lehmann, 2006; Noether, 1987).

# Poder da amostra para Wilcoxon não pareado (aproximação pelo teste t)
pwr.t.test(n = 26, d = 0.5*0.86, sig.level = 0.05, type = "two.sample")
## 
##      Two-sample t test power calculation 
## 
##               n = 26
##               d = 0.43
##       sig.level = 0.05
##           power = 0.3304646
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

23.1.4.3 c) Wilcoxon pareado

# Tamanho da amostra para Wilcoxon pareado (aproximação pelo teste t pareado)
pwr.t.test(d = 0.5, power = 0.8, sig.level = 0.05, type = "paired")
## 
##      Paired t test power calculation 
## 
##               n = 33.36713
##               d = 0.5
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number of *pairs*
# Poder da amostra para Wilcoxon não pareado (aproximação pelo teste t)
pwr.t.test(n = 26, d = 0.5*0.86, sig.level = 0.05, type = "two.sample")
## 
##      Two-sample t test power calculation 
## 
##               n = 26
##               d = 0.43
##       sig.level = 0.05
##           power = 0.3304646
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Atenção: O d de Cohen foi criado para testes paramétricos, como o teste t. Para testes não paramétricos (Wilcoxon), utilize medidas específicas, pois a interpretação do d não se aplica ao contexto de ranks.

23.1.5 Argumentos principais da função pwr.t.test()

A função pwr.t.test() possui os seguintes argumentos principais:

  • n: tamanho da amostra em cada grupo (ou número de pares, para teste pareado)
  • d: tamanho do efeito (diferença padronizada entre grupos)
  • power: poder estatístico desejado
  • sig.level: nível de significância (geralmente 0.05)
  • type: tipo de teste t: "two.sample", "paired" ou "one.sample"

Dica: Deixe como NULL o parâmetro que você deseja calcular. - Para calcular o tamanho do efeito: d = NULL - Para calcular o poder: power = NULL - Para calcular o tamanho da amostra: n = NULL

Exemplo para calcular o tamanho do efeito:

pwr.t.test(n = 26, d = NULL, power = 0.8, sig.level = 0.05, type = "two.sample")

Neste exemplo, o argumento d é o valor a ser calculado.

23.1.6 Grupos Desbalanceados: usando pwr.t2n.test()

Quando os grupos têm tamanhos diferentes, use pwr.t2n.test() para calcular o poder.

# Exemplo: grupo 1 com 95, grupo 2 com 30 observações
library(pwr)
pwr.t2n.test(n1 = 95, n2 = 30, d = 0.5, sig.level = 0.05)
## 
##      t test power calculation 
## 
##              n1 = 95
##              n2 = 30
##               d = 0.5
##       sig.level = 0.05
##           power = 0.6586749
##     alternative = two.sided
  • n1: tamanho do primeiro grupo
  • n2: tamanho do segundo grupo

Atenção: Grupos desbalanceados podem comprometer o poder do teste, aumentar a variância e dificultar a interpretação dos resultados. Sempre que possível, busque amostras equilibradas.

23.2 Tamanho do efeito em testes de Wilcoxon

O tamanho do efeito complementa a análise estatística, indicando a magnitude da diferença entre grupos. Para testes paramétricos (como o t), usa-se o d de Cohen. Para testes não paramétricos (Wilcoxon), utilize medidas apropriadas, como r de Wilcoxon e Delta de Cliff.

23.2.1 Por que NÃO usar d de Cohen no Wilcoxon?

  • O d de Cohen pressupõe distribuição normal e comparação direta de médias/desvios.
  • O Wilcoxon compara ranks, não médias.
  • Aplicar o d de Cohen em dados de Wilcoxon pode gerar interpretações erradas.

23.2.2 Medidas recomendadas para Wilcoxon:

  • r de Wilcoxon: Calculado com o pacote rstatix.
  • Cliff’s Delta: Disponível no pacote effsize.

23.2.2.1 r de Wilcoxon (Wilcoxon rank-sum, não pareado)

library(rstatix)
library(readr)

# Importe o banco de dados Pokemon
Pokemon <- read_csv("Pokemon.csv")

# Subconjunto com Pokémons verdes ou amarelos
dados_filtrados <- subset(Pokemon, Color %in% c("Green", "Yellow"))

# Verifique os dados após o filtro
print(table(dados_filtrados$Color))
## 
##  Green Yellow 
##     79     64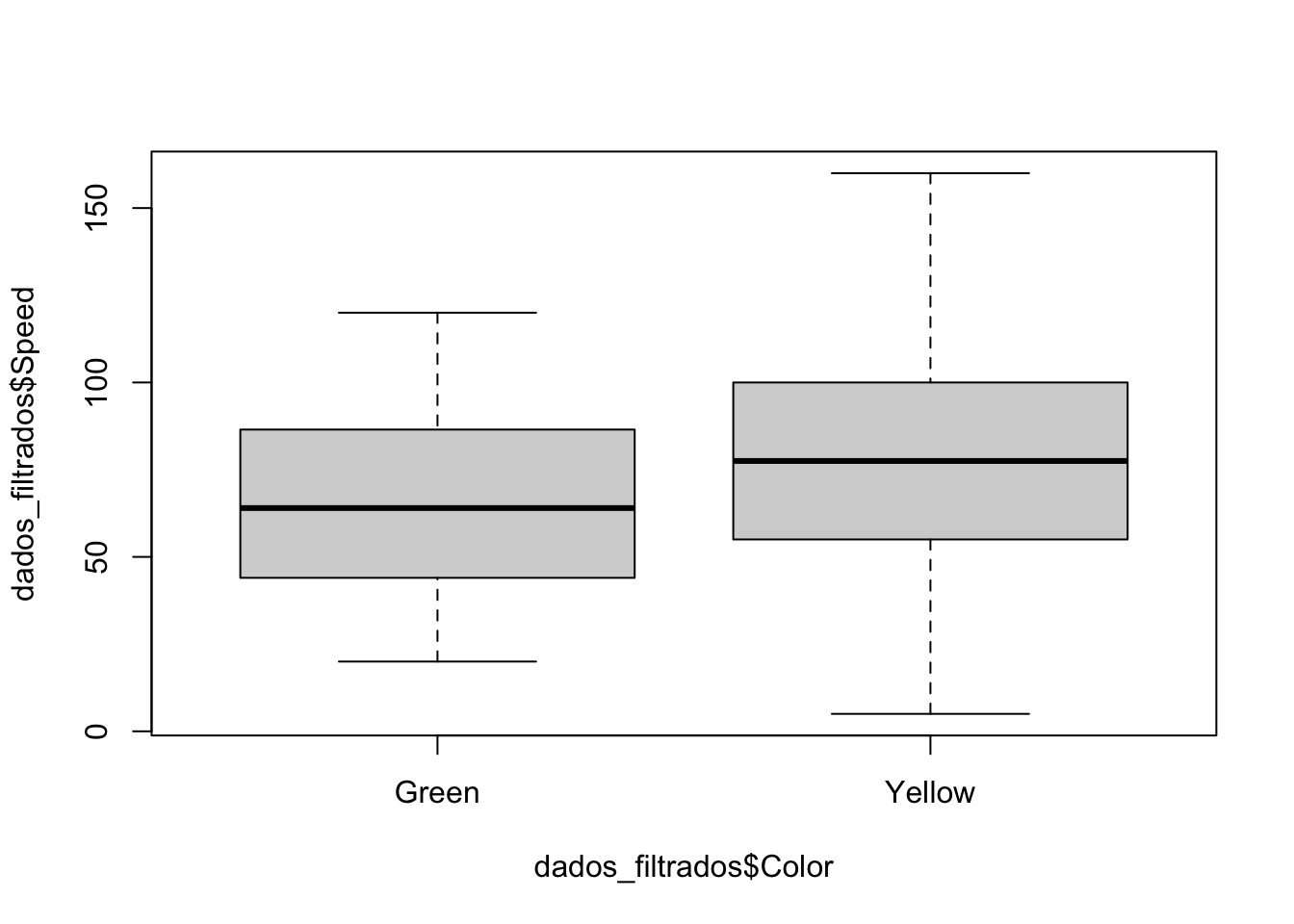
# Boxplot
boxplot(dados_filtrados$Speed ~ dados_filtrados$Color)

# Teste de Wilcoxon não pareado
wilcox.test(dados_filtrados$Speed ~ dados_filtrados$Color)
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  dados_filtrados$Speed by dados_filtrados$Color
## W = 1920.5, p-value = 0.01363
## alternative hypothesis: true location shift is not equal to 0
# Tamanho do efeito r de Wilcoxon para Green vs Yellow
wilcox_effsize(dados_filtrados, Speed ~ Color)
## # A tibble: 1 × 7
##   .y.   group1 group2 effsize    n1    n2 magnitude
## * <chr> <chr>  <chr>    <dbl> <int> <int> <ord>    
## 1 Speed Green  Yellow   0.206    79    64 small
levels(dados_filtrados$Color)
## NULL

A tabela apresentada é resultado da função wilcox_effsize() do pacote rstatix e resume o tamanho do efeito (r de Wilcoxon) para a comparação entre dois grupos (“Green” e “Yellow”) em relação à variável “Speed”. Veja como interpretar cada coluna:

  • .y.: variável de interesse analisada, neste caso, “Speed” (velocidade dos Pokémons).
  • group1: primeiro grupo comparado (“Green”).
  • group2: segundo grupo comparado (“Yellow”).
  • effsize: valor ABSOLUTO do tamanho de efeito calculado, aqui 0.206.
  • O resultado apresentado na coluna effsize é sempre positivo, independentemente da ordem dos grupos definidos na variável categórica.
  • n1: número de observações no grupo 1 (79 Pokémons verdes).
  • n2: número de observações no grupo 2 (64 Pokémons amarelos).
  • magnitude: classificação qualitativa do tamanho de efeito (“small”, ou seja, efeito pequeno).

Interpretação:
A diferença de velocidade entre Pokémons verdes e amarelos é estatisticamente significativa (W = 1920.5, p-value = 0.01363), porém de pequena magnitude (r = 0.206). Isso indica que, embora exista uma diferença, ela é discreta do ponto de vista prático.

No caso de teste pareado, acrescente o argumento paired = TRUE:

wilcox_effsize(dados, antes ~ depois, paired = TRUE)

23.2.2.2 Delta de Cliff

library(effsize)

# Calcule o Delta de Cliff
cliff.delta(dados_filtrados$Speed ~ dados_filtrados$Color)
## 
## Cliff's Delta
## 
## delta estimate: -0.2403085 (small)
## 95 percent confidence interval:
##       lower       upper 
## -0.41405995 -0.04966082

O Delta de Cliff estimado foi de -0,24, classificado como efeito pequeno (“small”). O intervalo de confiança de 95% vai de aproximadamente -0,41 a -0,05, indicando que, com alta confiança, o efeito verdadeiro é negativo e pequeno.

  • Sinal negativo: Indica que o grupo “Yellow” tende a apresentar velocidades maiores do que o grupo “Green”. Ou seja, ao comparar aleatoriamente um Pokémon amarelo com um verde, é mais provável que o amarelo tenha uma velocidade superior.
  • Magnitude pequena: O valor absoluto de -0,24 mostra que a diferença entre os grupos existe, mas é de pouca relevância prática.
  • Intervalo de confiança não inclui zero: Como o intervalo vai de -0,41 a -0,05, podemos afirmar que existe uma diferença real entre os grupos, embora seja pequena.
  • Interpretação prática: Apesar de haver uma diferença estatística, ela não é marcante. É importante avaliar se essa diferença tem relevância biológica ou prática no contexto do seu estudo.

O Delta de Cliff indica que Pokémons amarelos tendem a ser um pouco mais rápidos do que os verdes, mas a diferença é pequena do ponto de vista prático.

23.2.3 Comparação entre o r de Wilcoxon e o Delta de Cliff

Quando realizamos testes não paramétricos para comparar grupos, como o teste de Wilcoxon (Mann-Whitney ou Wilcoxon pareado), é importante complementar o resultado do teste com uma medida de tamanho de efeito. As duas opções mais comuns são o r de Wilcoxon e o Delta de Cliff. Veja a seguir uma comparação entre elas:

23.2.4 r de Wilcoxon

  • Definição: Mede a magnitude da diferença entre grupos com base nos postos (ranks) dos dados. O cálculo é semelhante ao coeficiente de correlação de Pearson, mas aplicado a dados não paramétricos.
  • Variação dos valores: O r de Wilcoxon varia de -1 a 1.
    • Valores próximos de 0 indicam pouca diferença entre grupos.
    • Valores próximos de -1 ou 1 indicam diferenças muito grandes.
    • O sinal indica a direção da diferença.

Qualificação dos valores, segundo Cohen (1988):

Valor absoluto de \(r\) Interpretação
aproximadamente 0,10 Pequeno
aproximadamente 0,30 Moderado
maior ou igual 0,50 Grande

Exemplos:

  • Efeito pequeno:
    Se o valor absoluto de r estiver próximo de 0,10, a diferença entre os grupos é pequena.
    (Exemplo: |r| = 0,10 → efeito pequeno)

  • Efeito moderado:
    Se o valor absoluto de r estiver próximo de 0,30, a diferença entre os grupos é moderada.
    (Exemplo: |r| = 0,30 → efeito moderado)

  • Efeito grande:
    Se o valor absoluto de r for igual ou superior a 0,50, a diferença é grande.
    (Exemplo: |r| = 0,55 → efeito grande)

23.2.5 Delta de Cliff (\(\delta\))

  • Definição: Mede a probabilidade de um valor de um grupo ser maior do que de outro grupo, subtraída da probabilidade contrária. É totalmente não paramétrico e não depende de distribuição, sendo adequado para variáveis ordinais ou dados assimétricos.
  • Variação dos valores: O Delta de Cliff varia de -1 a 1.
    • Valor 0: não há diferença entre os grupos.
    • Valor positivo: o grupo 1 tende a ter valores maiores que o grupo 2.
    • Valor negativo: o grupo 2 tende a ter valores maiores que o grupo 1.
  • Como interpretar os valores do Delta de Cliff?
    O Delta de Cliff mostra o tamanho da diferença entre dois grupos. O mais comum é considerar o valor absoluto de \(\delta\) (ou seja, ignorar se é positivo ou negativo e olhar só para o tamanho do número).

Classificação da magnitude do efeito, segundo Romano et al. (2006)

Valor absoluto de \(\delta\) Interpretação
menor que 0.147 Desprezível
de 0.147 e menor que 0.33 Pequeno
de 0.33 e menor que 0.474 Médio
maior ou igual a 0.474 Grande

Exemplos:

  • Efeito desprezível:
    Se o valor absoluto do delta for menor que 0,147, a diferença entre os grupos é desprezível.
    (Exemplo: |\(\delta\)| = 0,10 → efeito desprezível)

  • Efeito pequeno:
    Se o valor absoluto do delta for igual ou maior que 0,147 e menor que 0,33, a diferença é pequena.
    (Exemplo: |\(\delta\)| = 0,20 → efeito pequeno)

  • Efeito médio:
    Se o valor absoluto do delta for igual ou maior que 0,33 e menor que 0,474, a diferença é média.
    (Exemplo: |\(\delta\)| = 0,40 → efeito médio)

  • Efeito grande:
    Se o valor absoluto do delta for igual ou maior que 0,474, a diferença é grande.
    (Exemplo: |\(\delta\)| = 0,50 → efeito grande)

Resumindo:
Quanto mais próximo de zero, menor a diferença. Quanto mais próximo de 1 (ou -1), maior a diferença entre os grupos.

Dica: Sempre use o valor absoluto, ou seja, olhe apenas para o tamanho do número, sem se preocupar se ele é positivo ou negativo.

23.2.6 Qual é melhor usar?

  • Ambos são válidos e amplamente aceitos para dados não paramétricos.
  • O r de Wilcoxon é intuitivo se você já está acostumado com o coeficiente de correlação, e é facilmente interpretável em contextos onde se deseja uma analogia ao r de Pearson.
  • O Delta de Cliff é mais robusto em situações com muitos empates, diferentes tamanhos de grupo ou dados ordinais, e fornece uma interpretação mais direta da diferença de probabilidades entre grupos.
  • Recomendação prática:
    • Para estudos com dados ordenados, amostras desbalanceadas ou muitos empates, o Delta de Cliff pode ser preferido.
    • Se você busca uma medida análoga ao r de Pearson para facilitar comparações, use o r de Wilcoxon.
    • Em muitos casos, apresentar ambos os valores enriquece a interpretação dos resultados.

Não existe uma medida “melhor” de forma absoluta; a escolha depende do contexto do estudo e das características dos dados. Ambas são úteis para interpretar a relevância prática das diferenças identificadas em testes não paramétricos.

Nota: Para a comparação entre os grupos Green e Yellow na variável Speed, o tamanho de efeito calculado pelo r de Wilcoxon foi 0,206 (efeito pequeno), enquanto o delta de Cliff foi -0,240 (efeito pequeno, IC 95%: -0,414 a -0,050). É esperado que os valores numéricos dessas métricas diferem, pois são baseados em cálculos estatísticos distintos, mas ambos apontam para uma diferença de pequena magnitude entre os grupos.

No entanto, é importante destacar que, neste caso, o valor negativo do delta de Cliff está condizente com o observado no boxplot: o grupo Yellow tende a apresentar valores de Speed ligeiramente maiores que o grupo Green, o que é evidenciado pela direção negativa do delta.

Esse alinhamento entre o resultado numérico do delta de Cliff e a visualização gráfica reforça a importância de sempre analisar os dados de forma complementar, utilizando tanto medidas estatísticas quanto representações visuais (como boxplots). A visualização gráfica pode revelar padrões, tendências e assimetrias que enriquecem a interpretação do tamanho de efeito e facilitam a comunicação dos resultados.