Capítulo 24 Teste de Normalidade

Antes de aplicar muitos testes estatísticos, é importante verificar se os dados seguem uma distribuição normal (ou “distribuição gaussiana”). Essa etapa é fundamental porque vários testes paramétricos (como o teste t de Student e a ANOVA) assumem a normalidade dos dados. Quando essa condição não é atendida, a escolha do teste estatístico pode mudar para opções não paramétricas.

24.1 Hipóteses nos Testes de Normalidade

Todo teste de normalidade avalia as seguintes hipóteses:

  • Hipótese Nula (H₀): Os dados seguem uma distribuição normal.

  • Hipótese Alternativa (H₁): Os dados não seguem uma distribuição normal.

  • Se o valor de p for menor que 0,05: Não rejeitamos a hipótese nula. Os dados podem ser tratados como normais.

  • Se o valor de p for maior ou igual 0,05: Rejeitamos a hipótese nula. Os dados não seguem distribuição normal.

24.2 Principais Testes de Normalidade

Abaixo estão os testes de normalidade mais conhecidos, quando são mais recomendados e os pacotes em R:

Teste Quando Usar Pacote no R
Shapiro-Wilk Amostras pequenas e médias (n < 50 até ~ 2000) stats
Kolmogorov-Smirnov (K-S) Amostras maiores; pode comparar duas distribuições, mas menos potente para normalidade stats
Lilliefors Versão do K-S ajustado para média e desvio amostrais nortest
Anderson-Darling Mais sensível nas caudas da distribuição; recomendado para médias e grandes amostras nortest
Jarque-Bera Teste baseado em assimetria (skewness) e curtose (kurtosis); comum em econometria tseries
D’Agostino-Pearson Avalia assimetria e curtose em conjunto; recomendado para médias e grandes amostras moments

24.2.1 Dicas de Uso

  • Para amostras pequenas (n < 50): prefira o Shapiro-Wilk (função shapiro.test() do pacote base stats).
  • Para amostras médias a grandes: considere Anderson-Darling (ad.test() do pacote nortest) ou D’Agostino-Pearson (agostino.test() do pacote moments).
  • O Kolmogorov-Smirnov (ks.test()) é mais geral, mas menos recomendado quando a média e desvio padrão são estimados dos próprios dados.
  • O Lilliefors (lillie.test() do pacote nortest) é uma boa alternativa ao K-S para dados amostrais.
  • Para análises em econometria ou séries temporais, o Jarque-Bera (jarque.bera.test() do pacote tseries) é bastante utilizado.

24.2.2 Exemplo Prático em R

#install.packages("nortest")
#install.packages("moments")

# Importe o banco de dados Pokemon
library(readr)
Pokemon <- read_csv("Pokemon.csv")

# Veja o QQ
qqnorm(Pokemon$Speed)
qqline(Pokemon$Speed)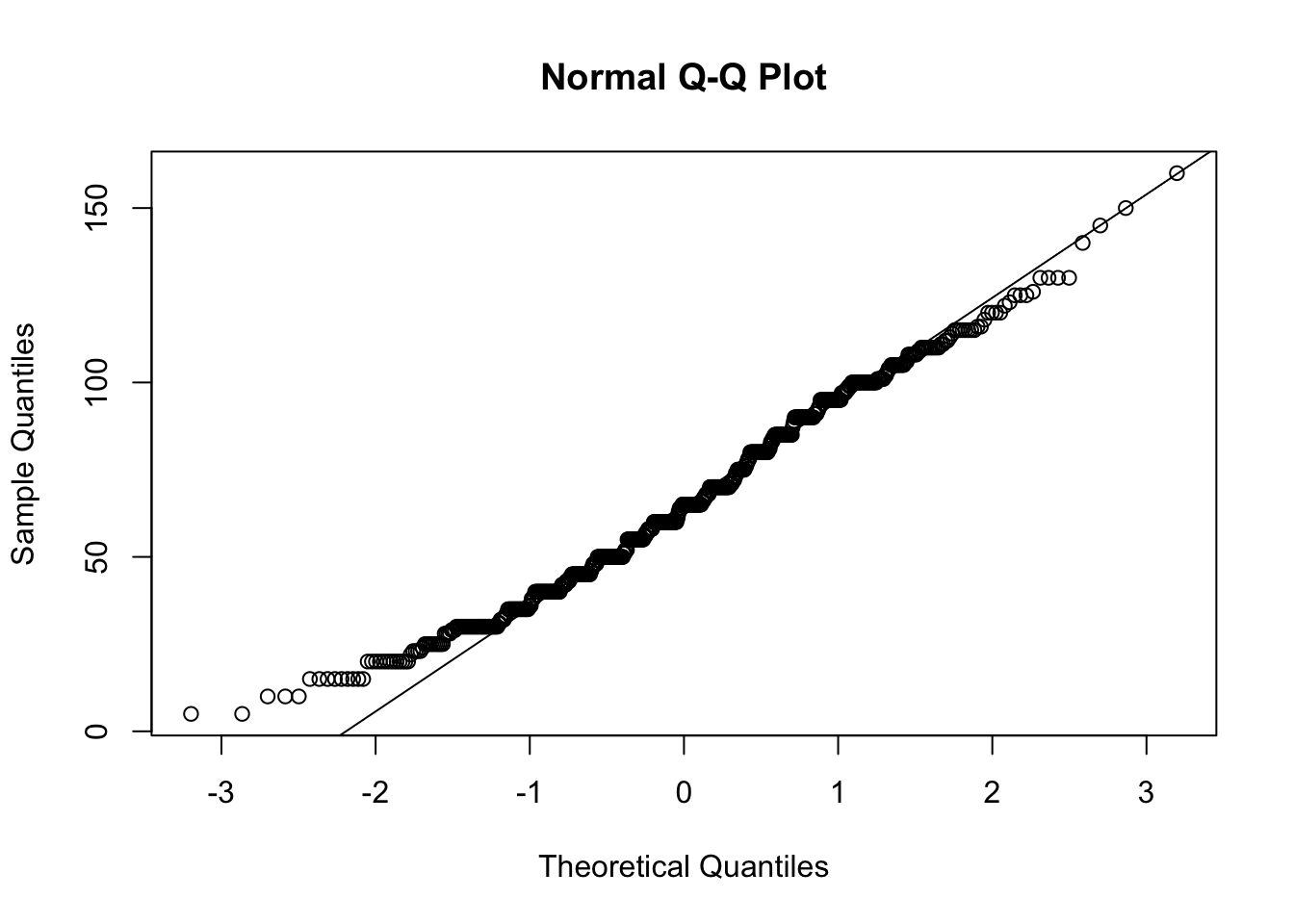

# Shapiro-Wilk
shapiro.test(Pokemon$Speed)
## 
##  Shapiro-Wilk normality test
## 
## data:  Pokemon$Speed
## W = 0.98574, p-value = 1.757e-06
# Anderson-Darling
library(nortest)
ad.test(Pokemon$Speed)
## 
##  Anderson-Darling normality test
## 
## data:  Pokemon$Speed
## A = 3.0665, p-value = 1.064e-07
# Lilliefors
lillie.test(Pokemon$Speed)
## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  Pokemon$Speed
## D = 0.06446, p-value = 1.662e-07
# D'Agostino
library(moments)
agostino.test(Pokemon$Speed)
## 
##  D'Agostino skewness test
## 
## data:  Pokemon$Speed
## skew = 0.27799, z = 3.02335, p-value = 0.0025
## alternative hypothesis: data have a skewness

Resumo

  • Sempre comece analisando a normalidade dos seus dados.
  • Escolha o teste de acordo com o tamanho da amostra e o objetivo da análise.
  • Use gráficos (histograma, boxplot e principalmente o QQ) junto com testes estatísticos para uma análise mais completa.

Importante: Testes de normalidade são sensíveis ao tamanho da amostra. Em amostras muito grandes, pequenas desvios podem resultar em p-valores baixos; em amostras pequenas, a potência dos testes é baixa.

24.3 Assimetria e Curtose: O que são e por que são importantes?

Quando analisamos dados, é importante entender não só a média e o desvio padrão, mas também o formato da distribuição dos valores. Duas medidas ajudam muito nisso: assimetria e curtose. Vamos entender cada uma de forma simples:

24.3.1 O que é Assimetria (Skewness)?

A assimetria mostra se os dados estão “puxados” para algum lado, ou seja, se a distribuição tem uma cauda maior para a direita ou para a esquerda.

  • Assimetria zero: Os dados estão distribuídos de forma equilibrada ao redor da média (exemplo: distribuição normal perfeita).
  • Assimetria positiva (à direita): A cauda é mais longa à direita, ou seja, há mais valores extremos acima da média.
  • Assimetria negativa (à esquerda): A cauda é mais longa à esquerda, há mais valores extremos abaixo da média.

Por que isso importa?
A distribuição Normal é um exemplo de distribuição simétrica.

24.3.2 O que é Curtose (Kurtosis)?

A curtose indica o quanto a distribuição é “pontuda” ou “achatada” em relação à Distribuição Normal.

  • Curtose alta (leptocúrtica): Distribuição muito “pontuda”, com muitas observações próximas da média, mas também mais valores extremos (outliers).
  • Curtose baixa (platicúrtica): Distribuição mais achatada, com menos valores extremos.
  • Curtose média (mesocúrtica): Parecida com a distribuição normal.

Por que isso importa?
A presença de muita curtose (valores muito altos ou baixos) pode indicar que há mais outliers do que o esperado, o que também pode afetar os resultados de testes estatísticos.

  • Assimetria: mostra se a distribuição “pende” para um lado.
  • Curtose: mostra se a distribuição é “pontuda” e cheia de extremos, ou mais “achatada”.

Essas duas medidas ajudam a entender melhor o comportamento dos seus dados e garantem que você escolha os testes estatísticos mais adequados para a sua análise!