Capítulo 27 Regressão
A regressão é uma técnica estatística usada para estudar a relação entre uma variável de interesse (chamada de variável dependente ou resposta) e uma ou mais variáveis que podem influenciá-la (chamadas de variáveis independentes ou preditoras). O objetivo principal é prever ou explicar o comportamento da variável resposta a partir das informações das variáveis preditoras.
Regressão Linear Simples:
É o tipo mais básico de regressão, analisando a relação entre duas variáveis: uma resposta (por exemplo, peso) e uma preditora (por exemplo, altura). A relação é representada por uma linha reta:
\[
\text{Resposta} = a + b \times \text{Preditora}
\]
Exemplo: Prever o peso de uma pessoa a partir de sua altura. O modelo estima qual seria o peso esperado para cada altura.
Regressão Linear Múltipla:
Quando queremos analisar o efeito de duas ou mais variáveis preditoras sobre a variável resposta, usamos a regressão linear múltipla. A equação fica:
\[
\text{Resposta} = a + b_1 \times \text{Preditora}_1 + b_2 \times \text{Preditora}_2 + \ldots
\]
Exemplo: Prever o preço de uma casa considerando área, número de quartos e localização.
Regressão Logística:
É usada quando a resposta é categórica, por exemplo: sim/não, doente/sadio, aprovado/reprovado. Em vez de prever um número, ela estima a probabilidade de um determinado evento ocorrer. Exemplo: Prever a chance de um paciente ter uma certa doença com base em exames. O resultado é sempre um valor entre 0 e 1 (uma probabilidade).
Outros Modelos de Regressão:
Além dos modelos acima, existem outros tipos de regressão para diferentes situações, como:
- Regressão de Poisson: para contagem de eventos (exemplo: número de acidentes por mês);
- Regressão de Prais-Winsten: utilizada em séries temporais, especialmente quando os dados têm dependência ao longo do tempo (como dados econômicos mensais);
- Regressão polinomial: ajusta curvas em vez de retas, para relações não-lineares;
- Regressão robusta, Ridge, Lasso: abordam problemas específicos como dados com valores extremos ou quando há muitas variáveis preditoras.
Em resumo, a regressão é uma ferramenta poderosa e versátil, útil em diferentes áreas como saúde, economia, educação e ciências sociais. Ela nos ajuda a compreender relações, prever resultados e tomar decisões baseadas em dados, mesmo sem precisar de conhecimentos avançados em matemática.
27.1 Regressão Linear Simples
A correlação responde à pergunta: “Existe relação linear? Qual a força e o sentido dessa relação?”
A regressão linear simples vai além: além de indicar se existe relação, ela fornece uma equação que quantifica e permite prever uma variável a partir da outra.
A equação tem a forma:
\[ Y = a + bX \]
onde: - Y: variável resposta (dependente) - X: variável explicativa (independente) - a: intercepto (valor esperado de Y quando X = 0) - b: inclinação (quanto Y varia, em média, a cada unidade de X)
A regressão responde à pergunta: “Como prever Y a partir de X?”
É comum estudar primeiro a correlação, pois ela mostra se vale a pena tentar ajustar um modelo de regressão linear.
27.1.1 Regressão Linear Simples no R
Como exemplo, vamos estudar a relação entre a frequência cardíaca (x, em batimentos por minuto - bpm) e o comprimento do intervalo QT (y, em milissegundos) de um eletrocardiograma (ECG). O intervalo QT representa o tempo que o coração leva para se despolarizar e repolarizar, sendo um importante marcador clínico.
Vamos considerar a seguinte amostra:
# Frequência cardíaca (bpm)
x <- c(60,75,62,68,84,97,66,65,86,78,93,75,88)
# Intervalo QT (ms)
y <- c(403,363,381,367,341,317,401,384,342,377,329,377,349)Vamos, primeiro, verificar o comportamento das variáveis pelo gráfio de dispersão:
plot(x, y,
xlab = "Frequência Cardíaca (bpm)",
ylab = "Intervalo QT (ms)",
pch = 19, col = "blue")
grid()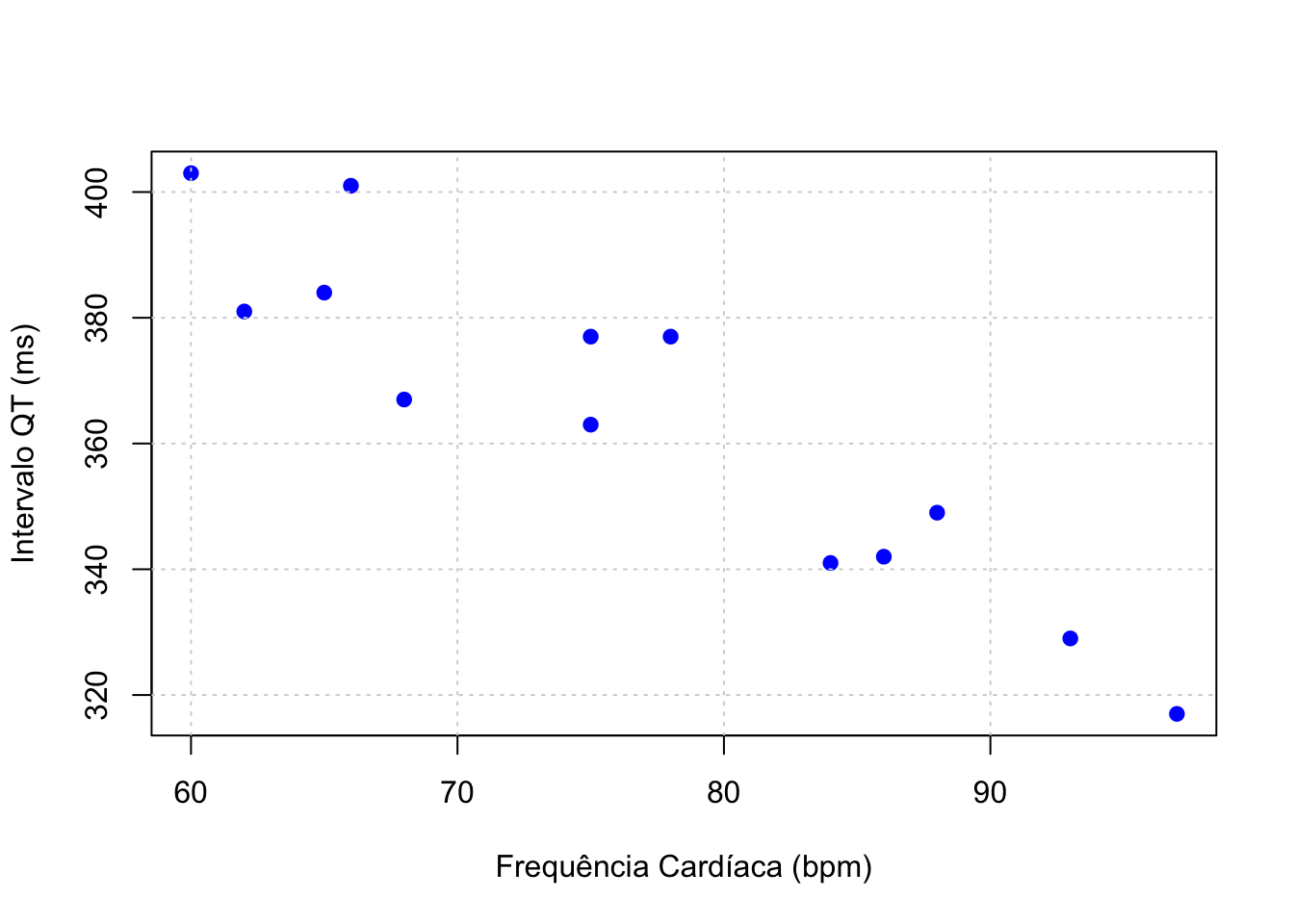
O teste de correlação nos fornece:
##
## Pearson's product-moment correlation
##
## data: x and y
## t = -8.2944, df = 11, p-value = 4.625e-06
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.9787673 -0.7730054
## sample estimates:
## cor
## -0.9285203- Coeficiente de correlação (r): -0,93
- Valor de t: -8,29
- Graus de liberdade (df): 11
- Valor-p: 0,0000046
- Intervalo de confiança (95%): de -0,98 a -0,77
O que isso significa?
- Força e direção: O coeficiente de correlação de Pearson (r = -0,93) indica uma correlação negativa muito forte entre as variáveis x e y. Isso significa que, à medida que uma variável aumenta, a outra tende a diminuir de forma bastante consistente.
- Significância estatística: O valor-p (p < 0,001) mostra que essa correlação é estatisticamente significativa. Ou seja, é extremamente improvável que essa relação forte e negativa tenha ocorrido por acaso.
- Intervalo de confiança: O intervalo de -0,98 a -0,77 indica que, com 95% de confiança, a verdadeira correlação na população está dentro desse intervalo — sempre indicando uma relação negativa forte.
- Hipótese nula: Como o valor-p é muito pequeno, rejeitamos a hipótese nula de que não existe correlação linear entre x e y.
Como há uma correlação linear forte e significativa, faz sentido estudar um modelo de regressão linear para quantificar e prever a relação entre essas variáveis.
Para ajustarmos um modelo onde o intervalo QT é explicado pela frequência cardíaca no R, usamos a função lm(), onde lm significa linear model.
##
## Call:
## lm(formula = y ~ x)
##
## Coefficients:
## (Intercept) x
## 520.668 -2.044O modelo ajustado de regressão linear simples foi:
\[ \text{Intervalo QT} = 520,67 - 2,04 \times \text{Frequência Cardíaca} \]
Interpretação dos coeficientes:
Intercepto (520,67):
Este valor representa a estimativa do intervalo QT (em milissegundos) quando a frequência cardíaca (x) é zero. Embora uma frequência cardíaca de zero não faça sentido fisiológico, o intercepto é necessário para construir a reta de regressão e serve como referência matemática.Inclinação (-2,04):
Esse coeficiente indica que, para cada aumento de 1 batimento por minuto (bpm) na frequência cardíaca, o intervalo QT diminui, em média, cerca de 2,04 milissegundos.
Ou seja, existe uma relação negativa: quanto maior a frequência cardíaca, menor tende a ser o intervalo QT.
O resumo da regressão é obtido a partir da função summary()
##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.689 -5.418 -2.900 8.188 15.750
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 520.6683 19.1158 27.238 1.90e-11 ***
## x -2.0438 0.2464 -8.294 4.63e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.38 on 11 degrees of freedom
## Multiple R-squared: 0.8622, Adjusted R-squared: 0.8496
## F-statistic: 68.8 on 1 and 11 DF, p-value: 4.625e-06Valor-p para ambos os coeficientes (p < 0,001): Os dois coeficientes são significativos, ou seja, existe evidência estatística muito forte de que ambos são diferentes de zero.
R² (Multiple R-squared): 0,86: Aproximadamente 86% da variação do intervalo QT é explicada pela frequência cardíaca. É um valor alto, indicando que o modelo ajusta bem os dados.
R² Ajustado (0,85): Leva em conta o número de variáveis e tamanho da amostra, e também é alto.
Erro padrão residual (Residual standard error: 10,38): Mede o desvio médio dos pontos em relação à reta ajustada (quanto menor, melhor).
Resíduos: Representam a diferença entre os valores observados e os previstos pelo modelo. Os valores mínimos e máximos indicam a dispersão dos erros.
F-statistic: 68,8, p-value: 4,6e-06: Teste global do modelo, confirma que a relação encontrada é altamente significativa.
O modelo de regressão linear simples mostra que existe uma forte relação linear negativa e estatisticamente significativa entre a frequência cardíaca e o intervalo QT: quanto maior a frequência cardíaca, menor tende a ser o intervalo QT. O modelo explica a maior parte da variação dos dados, sendo útil para previsões e interpretações clínicas dessa relação.
O intervalos de confiança para os coeficientes da reta é dado por:
## 2.5 % 97.5 %
## (Intercept) 478.594702 562.741896
## x -2.586164 -1.501475Intercepto (a):
O intervalo de confiança de 95% para o intercepto vai de 478,59 a 562,74. Isso significa que, com 95% de confiança, o verdadeiro valor do intercepto está dentro desse intervalo. O intercepto representa o valor estimado do intervalo QT quando a frequência cardíaca é zero (valor teórico/matemático).Inclinação (b):
O intervalo de confiança de 95% para a inclinação vai de -2,59 a -1,50. Como o intervalo é totalmente negativo, reforça que a relação entre frequência cardíaca e intervalo QT é negativa: a cada aumento de 1 bpm na frequência cardíaca, o intervalo QT diminui, em média, entre 1,50 e 2,59 ms.
Limitações e Cuidados na Regressão Linear
Apesar do modelo indicar uma associação significativa, é importante considerar algumas limitações e pontos de atenção:
- Extrapolação: O modelo é válido apenas para a faixa de dados observados. Prever valores de QT para frequências cardíacas muito fora do intervalo observado pode gerar resultados sem sentido.
- Suposições do modelo:
- Linearidade: A relação entre as variáveis deve ser aproximadamente linear.
- Normalidade dos resíduos: Os resíduos (erros) devem ser aproximadamente distribuídos normalmente.
- Homoscedasticidade: A variância dos resíduos deve ser constante ao longo dos valores previstos.
- Independência: As observações devem ser independentes entre si. Recomenda-se sempre checar essas suposições usando gráficos de resíduos e testes estatísticos.
- Possíveis valores extremos (outliers): Valores muito diferentes dos demais podem influenciar fortemente o ajuste, distorcendo os resultados.
- Correlação não implica causalidade: A regressão mostra associação, mas não garante que uma variável causa a outra.
27.1.2 O que deve ser checado ao ajustar uma regressão linear?
- Gráfico de resíduos: Para avaliar linearidade, homoscedasticidade e detectar outliers.
- Histograma/QQ-plot dos resíduos: Para verificar a normalidade dos resíduos.
- Verificar influências: Avaliar se algum ponto influencia demais o resultado (diagnóstico de outliers/influência).
- Intervalos de confiança: Analisar a precisão das estimativas dos parâmetros.
- R² e R² ajustado: Avaliar o quanto do comportamento da variável resposta é explicado pelo modelo.
27.2 Regressão Linear Múltipla
Depois de entender a regressão linear simples, é fácil expandir para a regressão linear múltipla, onde podemos incluir mais de uma variável preditora para explicar a variável resposta. No nosso exemplo, além da frequência cardíaca (x), vamos acrescentar a idade dos indivíduos (z), que também pode influenciar o intervalo QT do eletrocardiograma (y).
Vamos supor os seguintes valores de idade para os mesmos indivíduos:
# Frequência cardíaca (bpm)
x <- c(60,75,62,68,84,97,66,65,86,78,93,75,88)
# Intervalo QT (ms)
y <- c(403,363,381,367,341,317,401,384,342,377,329,377,349)
# Idade (anos) - exemplo hipotético
z <- c(25,40,30,22,53,60,28,27,50,35,59,41,55)Vamos ajustar agora um modelo que considera tanto a frequência cardíaca quanto a idade como preditoras do intervalo QT:
- O modelo ajustado tem a forma: \[ \text{QT} = a + b_1 \times \text{Frequência Cardíaca (x)} + b_2 \times \text{Idade (z)} \]
##
## Call:
## lm(formula = y ~ x + z)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.055 -5.737 -2.952 8.566 15.082
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 514.3929 37.2473 13.810 7.72e-08 ***
## x -1.8827 0.8466 -2.224 0.0504 .
## z -0.1505 0.7534 -0.200 0.8457
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.87 on 10 degrees of freedom
## Multiple R-squared: 0.8627, Adjusted R-squared: 0.8352
## F-statistic: 31.42 on 2 and 10 DF, p-value: 4.88e-05Modelo ajustado:
\[
\text{QT} = 514,39 - 1,88 \times \text{Frequência Cardíaca (x)} - 0,15 \times \text{Idade (z)}
\]
Intercepto (514,39):
Valor estimado do QT quando frequência cardíaca e idade são zero (valor teórico, apenas referência matemática).Frequência Cardíaca (x):
O coeficiente é -1,88, ou seja, para cada aumento de 1 bpm, o QT diminui em média 1,88 ms, mantendo a idade constante.
O valor-p (0,0504) é limítrofe, indicando que a influência da frequência cardíaca sobre o QT ainda é significativa, mas no limite do nível de significância tradicional (5%).Idade (z):
O coeficiente é -0,15, ou seja, para cada aumento de 1 ano de idade, o QT diminui, em média, 0,15 ms, mantendo a frequência cardíaca constante.
No entanto, o valor-p (0,8457) mostra que essa associação não é estatisticamente significativa — ou seja, não há evidência de que a idade tenha efeito relevante sobre o QT neste conjunto de dados.
Qualidade do ajuste
- R² (0,86):
Aproximadamente 86% da variação do QT é explicada pelo modelo com as duas variáveis preditoras, indicando bom ajuste. - R² ajustado (0,83):
Leva em conta o número de variáveis, também indicando bom ajuste. - Erro padrão residual (10,87):
Média dos desvios dos pontos em relação à reta ajustada, semelhante ao modelo simples.
Análise dos resíduos
- A distribuição dos resíduos sugere que o modelo está adequado, mas sempre é recomendado visualizar os gráficos de resíduos para avaliar possíveis violações das suposições.
Teste F
- F-statistic: 31,42, p-value: 4,88e-05:
O modelo como um todo é altamente significativo, ou seja, pelo menos uma das variáveis preditoras está relacionada ao QT.
Conclusão
- O modelo de regressão múltipla mostra que, mantendo a idade constante, a frequência cardíaca segue sendo um preditor importante e significativo para o intervalo QT.
- A idade, por outro lado, não contribuiu de forma significativa para explicar o QT nesse exemplo.
- O ajuste da regressão múltipla no R é simples e a interpretação amplia a compreensão das relações entre várias variáveis e a resposta.
- Importante: Sempre verifique as suposições do modelo e a significância de cada preditor.
27.3 No R é fácil
A sintaxe para ajustar a regressão múltipla é muito parecida com a da simples, basta acrescentar as variáveis ao modelo:
Se quiser incluir ainda mais variáveis, basta adicioná-las na fórmula, separadas por +.
Visualização dos resíduos
É importante, como sempre, checar os resíduos para garantir que as suposições do modelo continuam válidas:
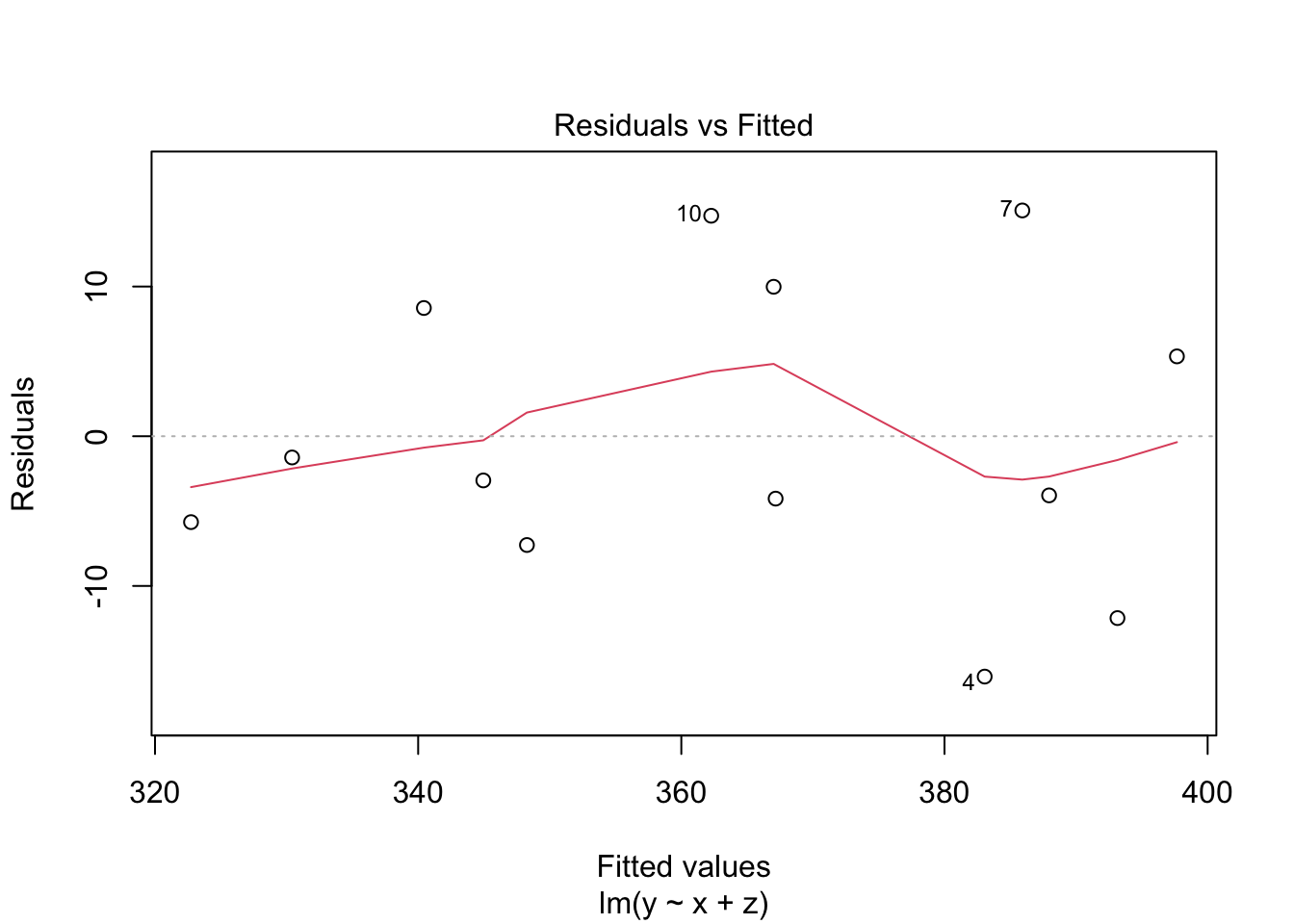
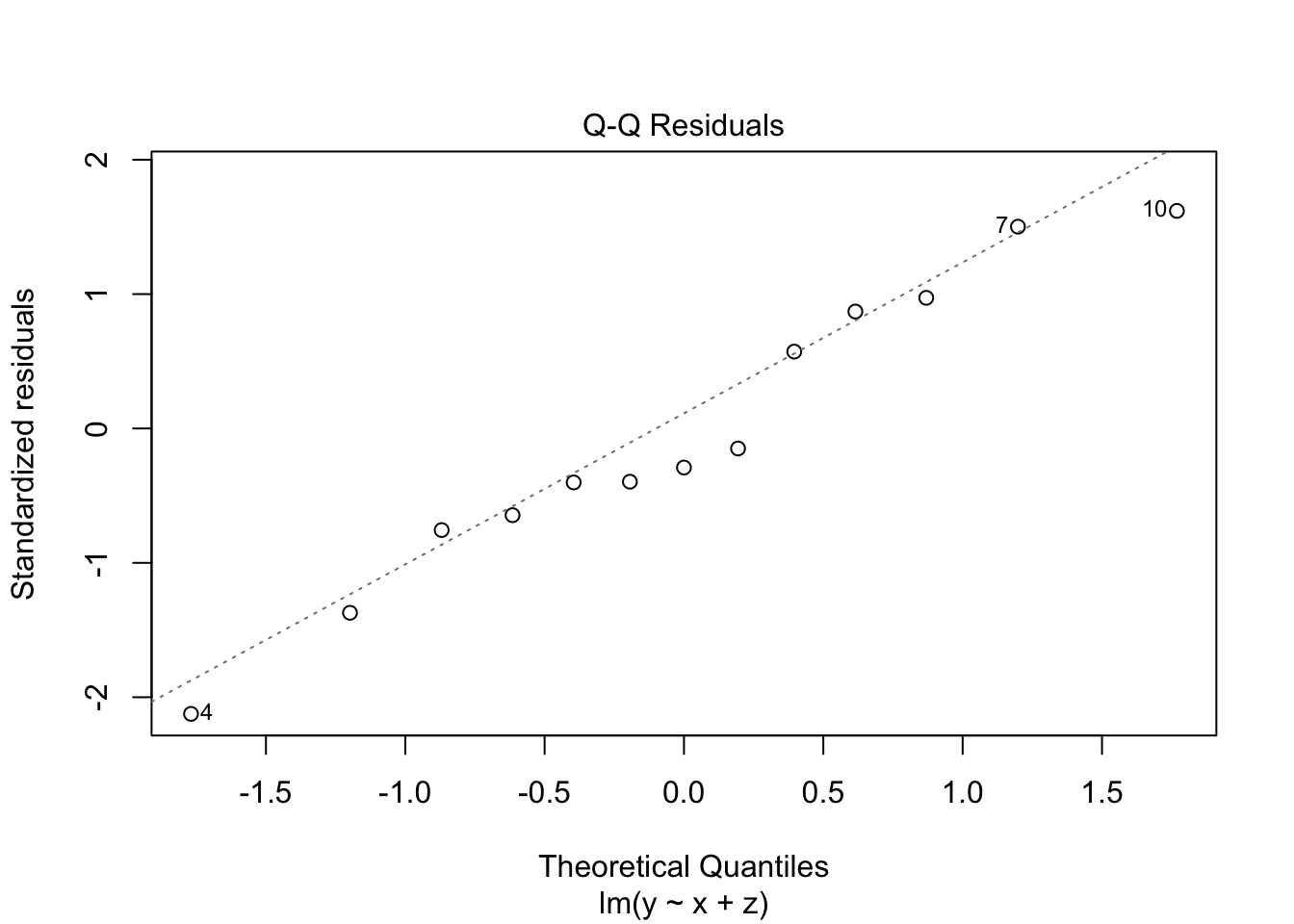
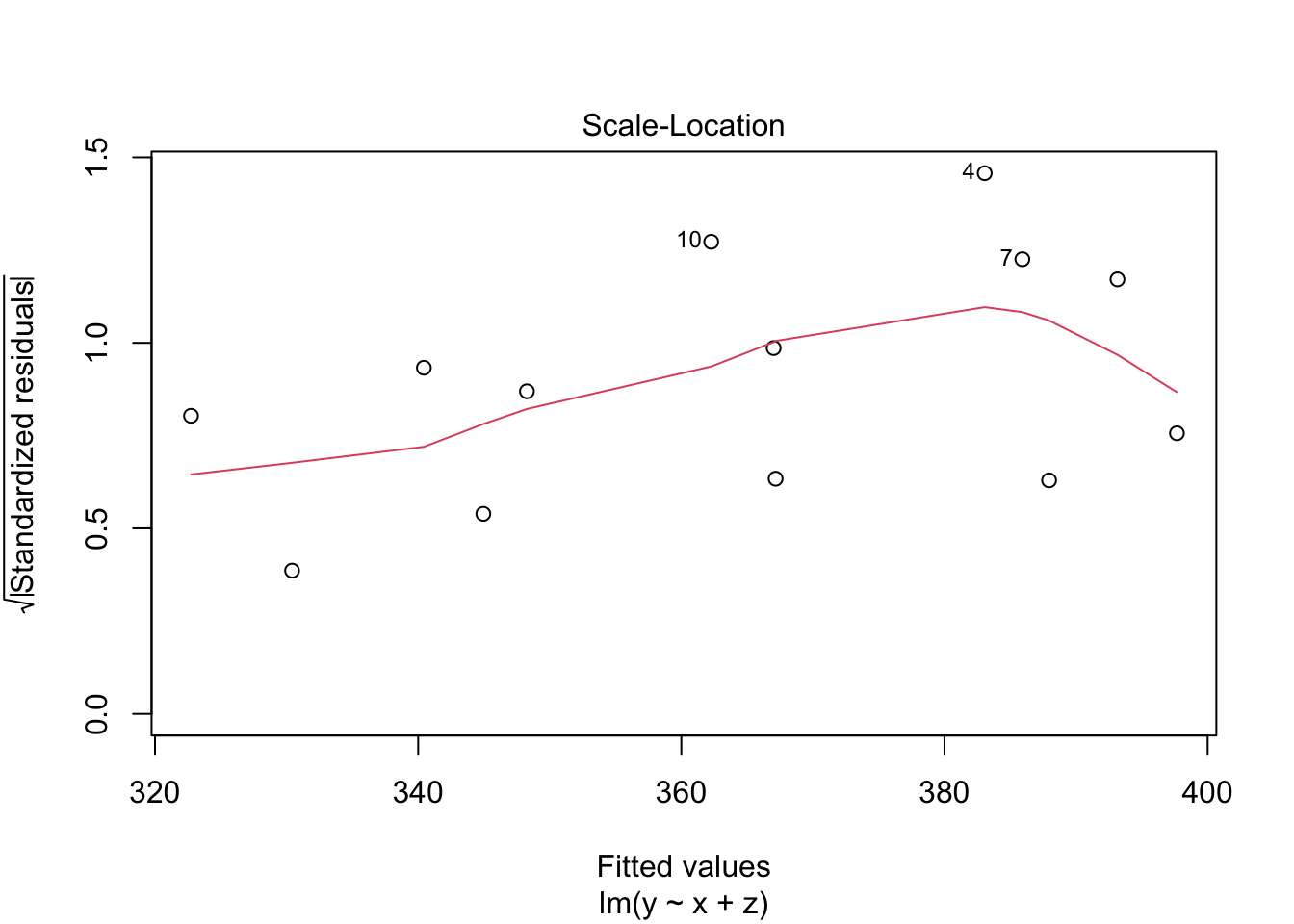
Resíduos vs Valores Ajustados
- Objetivo: Avaliar linearidade e homocedasticidade (variância constante dos resíduos).
- Interpretação: Os resíduos estão distribuídos de forma aproximadamente aleatória ao redor de zero, sem padrões claros. Isso sugere que a relação linear é adequada e que a variância dos resíduos é razoavelmente constante. Não há grandes evidências de problemas de ajuste, ainda que um ou outro ponto se afaste mais do centro (possíveis outliers).
Q-Q Plot dos Resíduos
- Objetivo: Verificar se os resíduos seguem uma distribuição normal (suposição importante para testes de hipóteses na regressão).
- Interpretação: Os pontos seguem bem a linha reta, indicando que a normalidade dos resíduos é atendida na maior parte dos casos. Pequenos desvios nas extremidades são toleráveis, especialmente com amostras pequenas, como neste exemplo.
Scale-Location (Homocedasticidade)
- Objetivo: Avaliar se a variância dos resíduos é constante para todos os valores ajustados (homocedasticidade).
- Interpretação: Os pontos estão relativamente dispersos de forma homogênea ao longo do eixo dos valores ajustados, sem formar um funil ou padrão crescente/decrescente marcante. Isso reforça que a suposição de homocedasticidade está sendo atendida.
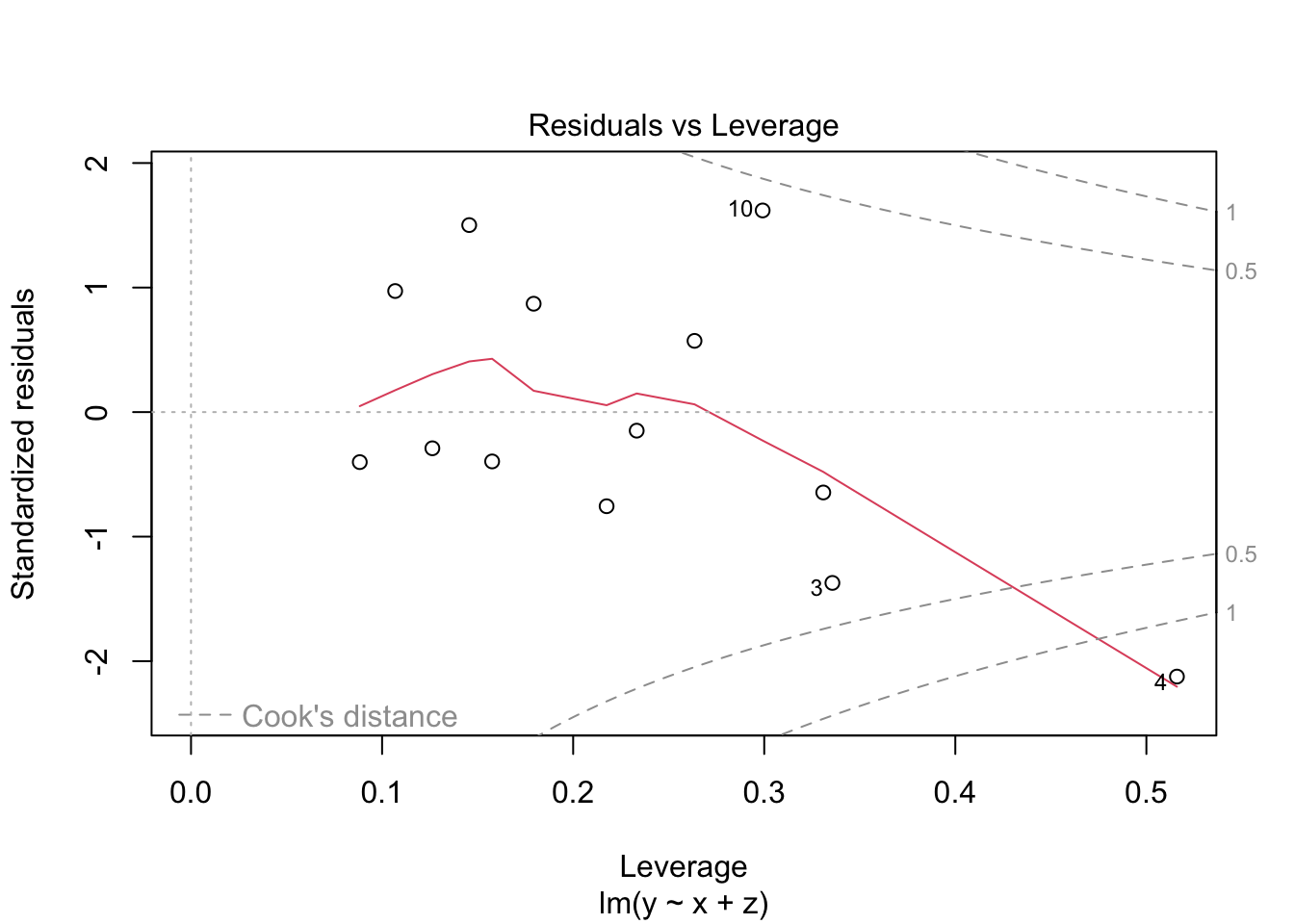
Resíduos Padronizados vs Leverage
- Objetivo: Identificar pontos com alto potencial de influência no modelo (outliers ou observações influentes).
- Interpretação: A maioria dos pontos está dentro dos limites aceitáveis de leverage e resíduos. Apenas um ou dois pontos apresentam valores de leverage mais altos, mas sem exceder drasticamente os limites de distância de Cook. Isso sugere que não há observações extremamente influentes comprometendo o modelo.
Os diagnósticos gráficos indicam que: - As suposições do modelo de regressão múltipla estão razoavelmente bem atendidas: linearidade, normalidade dos resíduos, homocedasticidade e ausência de pontos influentes extremos. - O modelo é adequado para os dados analisados, com apenas leves indícios de possíveis outliers, mas sem comprometer as conclusões.
27.4 Exercício
O exercício “nutrientes em cereais matinais” foi retirado do livro Estatística Básica de Larson & Farber.
A U.S. Food and Drug Administration (FDA) exige a rotulagem nutricional para a maioria dos alimentos. Sob os regulamentos da FDA, os produtores são obrigados a listar as quantidades de certos nutrientes em seus alimentos, tais como: calorias, açúcar, gordura e carboidratos. Essa informação nutricional é exibida em uma tabela na embalagem do alimento.
A Tabela mostra o teor nutricional para uma xícara de 21 cereais matinais diferentes.
C = calorias
S = açúcar em gramas
F = gordura em gramas
R = carboidratos em gramas
| C | S | F | R |
|---|---|---|---|
| 100 | 12 | 0.5 | 25 |
| 130 | 11 | 1.5 | 29 |
| 110 | 10 | 1.0 | 29 |
| 130 | 15 | 2.0 | 31 |
| 130 | 13 | 1.5 | 29 |
| 120 | 3 | 0.5 | 26 |
| 100 | 2 | 0.0 | 24 |
| 120 | 0 | 0.0 | 29 |
| 150 | 16 | 1.5 | 31 |
| 110 | 4 | 0.0 | 25 |
| 110 | 12 | 1.0 | 23 |
| 160 | 15 | 1.5 | 35 |
| 150 | 12 | 2.0 | 36 |
| 150 | 15 | 1.5 | 29 |
| 110 | 15 | 0.0 | 29 |
| 190 | 13 | 1.5 | 45 |
| 100 | 3 | 0.0 | 23 |
| 120 | 4 | 0.5 | 23 |
| 120 | 11 | 1.5 | 28 |
| 120 | 11 | 1.0 | 29 |
| 130 | 5 | 0.5 | 29 |
1. Use o R para obter um diagrama de dispersão dos seguintes pares \((x, y)\) no conjunto de dados.
- (Calorias, açúcar.)
- (Calorias, gordura.)
- (Calorias, carboidratos.)
- (Açúcar, gordura.)
- (Açúcar, carboidratos.)
- (Gordura, carboidratos.)
2. Dos diagramas de dispersão no Exercício 1, quais pares de variáveis parecem ter uma correlação linear forte?
3. Use o R para encontrar o coeficiente de correlação para cada par de variáveis no Exercício 1. Qual tem a correlação linear mais forte?
4. Use tecnologia para encontrar a equação de uma reta de regressão para os seguintes pares de variáveis.
- (Calorias, açúcar.)
- (Calorias, carboidratos.)
5. Use os resultados do Exercício 4 para prever o seguinte:
- O teor de açúcar de uma xícara de cereal que tem 120 calorias.
- O teor de carboidrato de uma xícara de cereal que tem 120 calorias.
6. Use tecnologia para encontrar as equações de regressão múltipla dos seguintes modelos:
- \(C = b + m_1S + m_2F + m_3R\)
- \(C = b + m_1S + m_2R\)
7. Use as equações do Exercício 6 para prever as calorias em 1 xícara de cereal que tem 7 gramas de açúcar; 0,5 grama de gordura e 31 gramas de carboidratos.