Capítulo 26 Correlação entre variáveis

A correlação é uma forma de medir o grau de relação entre duas variáveis. Quando duas variáveis estão correlacionadas, significa que podemos esperar que, ao mudar uma delas, a outra também sofra alguma alteração. Se ambas aumentam juntas, dizemos que a correlação é positiva; se uma aumenta enquanto a outra diminui, a correlação é negativa.

É importante destacar que a correlação indica apenas que as variáveis variam juntas, mas não prova que uma causa a mudança na outra. Outros fatores podem estar influenciando essa relação, ou pode ser apenas uma coincidência. Por isso, correlação mostra como as variáveis estão relacionadas, mas não estabelece uma relação de causa e efeito.

Na medicina, um exemplo clássico é investigar a correlação entre o índice de massa corporal (IMC) e a pressão arterial sistólica. Pesquisadores podem avaliar se pessoas com IMC mais elevado tendem a ter pressão arterial mais alta, o que ajuda a entender riscos cardiovasculares.

Na psicologia, pode-se analisar a correlação entre a pontuação em uma escala de ansiedade (por exemplo, a pontuação total em um questionário) e o número de horas de sono por noite. Essa relação ajuda a compreender como o sono influencia o nível de ansiedade.

Na educação física, um exemplo é estudar a correlação entre o tempo gasto em atividade física semanal (em horas) e a porcentagem de gordura corporal. Isso auxilia na avaliação do impacto do exercício sobre a composição corporal.

26.1 Tipos de Variáveis

Para analisar correlação, usamos variáveis numéricas (quantitativas ou qualitativas ordinais).

26.2 Diagrama de Dispersão

O diagrama de dispersão é um gráfico que permite visualizar a relação entre duas variáveis. A seguir, exemplos de diferentes padrões de correlação:

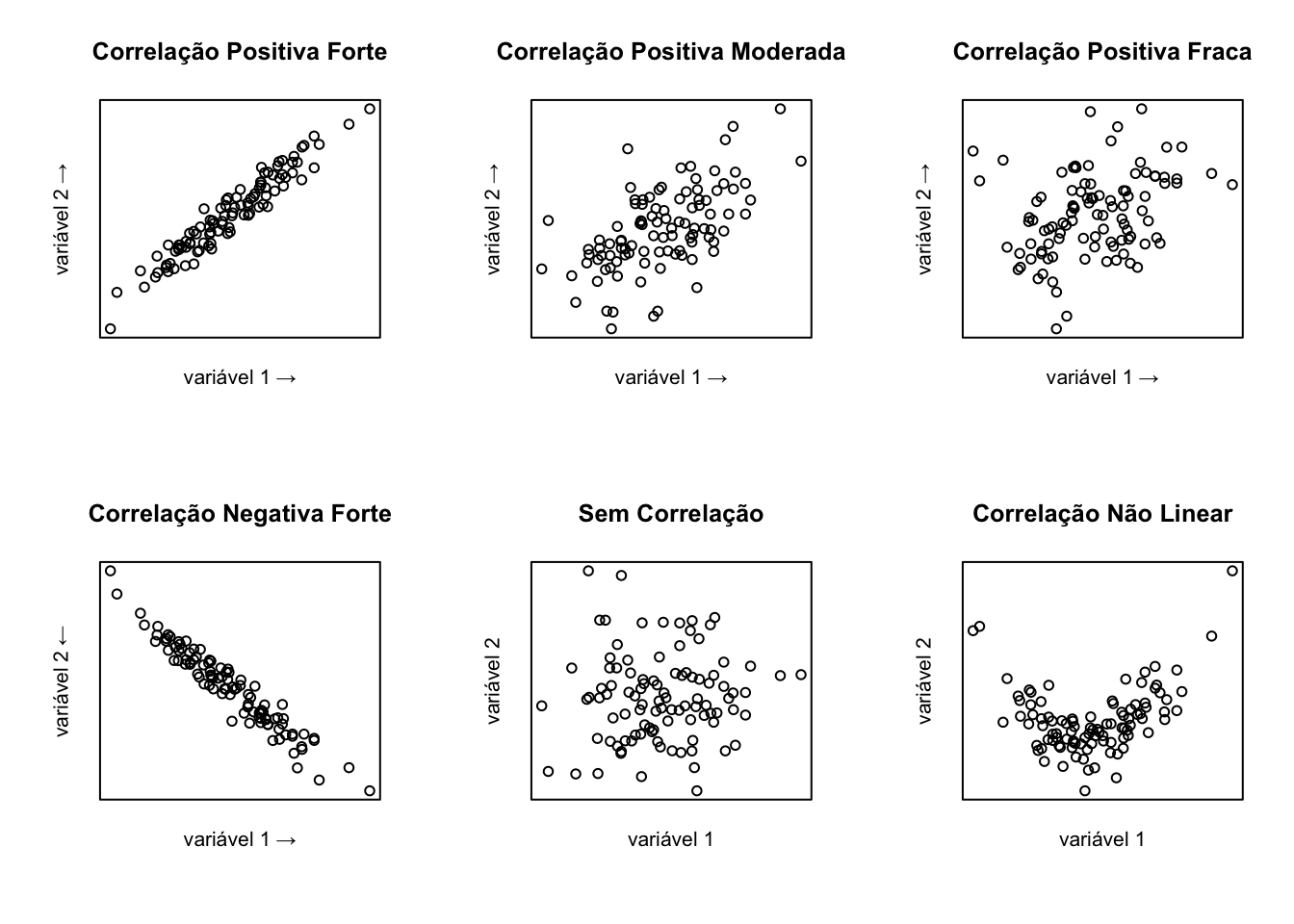
Para criar um gráfico de dispersão no R, você pode usar a função plot(). Os argumentos básicos que você deve fornecer entre os parênteses são:

  • “x”: um vetor numérico com os valores do eixo x (variável independente).
  • “y”: um vetor numérico com os valores do eixo y (variável dependente).

Ou seja, algo como: plot(x,y)

26.3 Coeficientes de Correlação

Existem diferentes métodos para medir a correlação entre variáveis, cada um adequado a tipos específicos de dados e relações. Os três tipos mais comuns são: a correlação de Pearson, que avalia a relação linear entre variáveis numéricas contínuas; a correlação de Spearman, que mede associações monotônicas usando postos, sendo indicada para dados ordinais ou quando a relação não é estritamente linear; e a correlação de Kendall, também baseada em postos, que é especialmente útil em amostras pequenas ou com muitos empates nos dados. Conhecer essas diferenças é fundamental para escolher o método mais apropriado em cada situação.

26.3.1 Coeficiente de Correlação de Pearson

O coeficiente de correlação de Pearson (\(r\)) é utilizado quando se deseja avaliar a relação linear entre duas variáveis quantitativas contínuas. Ele pressupõe que os dados de ambas as variáveis seguem uma distribuição normal (ou aproximadamente normal) e que a relação entre elas é linear, ou seja, uma linha reta pode descrever bem o padrão dos dados em um gráfico de dispersão. É sensível a outliers.

26.3.2 Coeficiente de Correlação de Spearman

O coeficiente de Spearman (\(\rho\)) avalia a força e a direção da associação entre duas variáveis com base em seus ranks (postos) em vez dos valores originais. Ele é indicado quando a relação entre as variáveis é monotônica, ou seja, conforme uma variável aumenta, a outra também aumenta ou diminui, mas não necessariamente de maneira linear. O Spearman é apropriado para dados que não seguem a normalidade ou para situações em que a relação não pode ser descrita por uma linha reta. Além disso, é menos sensível a outliers do que o Pearson.

26.3.3 Coeficiente de Correlação de Kendall

O coeficiente de Kendall (\(\tau\)) também se baseia nos postos dos dados, sendo utilizado para medir a força da associação entre duas variáveis. É especialmente útil em situações com pequenas amostras ou quando há muitos empates nos valores dos dados (valores iguais). Assim como o Spearman, o Kendall não exige normalidade dos dados e é apropriado para relações monotônicas. Em geral, o tau de Kendall é visto como mais robusto em amostras pequenas ou com muitos empates.

26.3.4 Interpretação dos Coeficientes

O valor a correlação varia de -1 (correlação negativa perfeita) a +1 (correlação positiva perfeita), sendo 0 a ausência de correlação linear.

Faixa de valores Interpretação
0,00 – 0,10 Desprezível
0,10 – 0,30 Fraca
0,30 – 0,50 Moderada
0,50 – 0,70 Forte
0,70 – 1,00 Muito forte

26.3.5 Exemplo no R

Vamos supor que temos os dados de 18 alunos: a quantidade de aulas frequentadas (de um total de 20) e suas notas finais na disciplina de Estatística (de 0 a 10).

# Vetor de presenças (número de aulas frequentadas)
presencas <- c(20, 18, 17, 19, 15, 16, 20, 18, 17, 19, 14, 15, 12, 16, 20, 13, 17, 18)

# Vetor de notas finais em Estatística
notas <- c(9.8, 9.0, 8.5, 9.5, 7.0, 7.5, 10.0, 8.7, 8.0, 9.2, 6.5, 7.2, 5.0, 7.8, 9.7, 6.0, 8.2, 8.8)
# Para calcular o r de Pearson
cor(presencas, notas, method = "pearson")
## [1] 0.992563
# Para calcular o rho de Spearman
cor(presencas, notas, method = "spearman")
## [1] 0.9922299
# Para calular o tau de Kendall
cor(presencas, notas, method = "kendall")
## [1] 0.9599837
# Dica: dá para abreviar o nome de cada método
# Para calcular o r de Pearson
cor(presencas, notas, method = "p")
## [1] 0.992563
# Para calcular o rho de Spearman
cor(presencas, notas, method = "s")
## [1] 0.9922299
#para calular o tau de Kendall
cor(presencas, notas, method = "k")
## [1] 0.9599837

26.4 Testes de Correlação

26.4.1 Pearson

  • H0: \(r = 0\) (não há correlação linear entre as variáveis “x” e “y”)
  • H1: \(r \neq 0\) (existe correlação)
cor.test(presencas, notas, method = "pearson")
## 
##  Pearson's product-moment correlation
## 
## data:  presencas and notas
## t = 32.615, df = 16, p-value = 4.597e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.9796700 0.9972906
## sample estimates:
##      cor 
## 0.992563

O teste de correlação de Pearson realizado entre as variáveis presencas e notas apresentou os seguintes resultados:

  • t = 32.615:
    Este é o valor do teste t calculado, que indica uma diferença extremamente significativa entre a correlação observada e a hipótese nula (correlação igual a zero). Quanto maior o valor de t, maior a evidência contra a hipótese nula.

  • df = 16:
    Refere-se aos graus de liberdade do teste, calculados por (n - 2), onde n é o número de pares de dados analisados. Neste caso, indica que havia 18 observações.

  • p-value = 4.597e-16:
    O valor-p extremamente baixo mostra que a probabilidade de obter uma correlação tão forte por acaso é praticamente nula. Portanto, a correlação é estatisticamente significativa.

  • alternative hypothesis: true correlation is not equal to 0:
    A hipótese alternativa testada é de que existe alguma correlação (positiva ou negativa) diferente de zero entre as variáveis.

  • 95 percent confidence interval: 0.9796700 a 0.9972906:
    O intervalo de confiança indica que, com 95% de certeza, o valor real da correlação populacional entre presencas e notas está entre aproximadamente 0,98 e 0,997. Isso é considerado uma correlação extremamente forte.

  • sample estimates: cor = 0.992563:
    O coeficiente de correlação de Pearson (\(r\)) observado foi de 0,99, indicando uma relação positiva, muito forte e praticamente perfeita: quanto maior o número de presenças, maior tende a ser a nota.

Resumo:
Os resultados mostram uma associação positiva fortíssima e estatisticamente significativa entre presenças e notas, sugerindo que alunos que frequentam mais tendem a obter notas mais altas.

26.4.2 Spearman

  • H0: \(\rho = 0\) (não há correlação entre as variáveis “x” e “y”)
  • H1: \(\rho \neq 0\) (existe correlação)
cor.test(presencas, notas, method = "spearman")
## 
##  Spearman's rank correlation rho
## 
## data:  presencas and notas
## S = 7.5293, p-value = 6.52e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.9922299

O teste de correlação de Spearman realizado entre as variáveis presencas e notas apresentou os seguintes resultados:

  • S = 7.5293:
    Este é o valor da estatística de teste S, usada no cálculo da correlação de Spearman. Ele reflete as diferenças nas posições (ranks) entre as duas variáveis analisadas.

  • p-value = 6.52e-16:
    O valor-p extremamente baixo indica que a probabilidade de observar uma correlação tão alta por acaso, caso não exista correlação real, é praticamente nula. Portanto, a correlação encontrada é estatisticamente significativa.

  • alternative hypothesis: true rho is not equal to 0:
    A hipótese alternativa do teste é de que o coeficiente de Spearman (\(\rho\)) é diferente de zero, ou seja, existe uma associação monotônica entre as variáveis.

  • sample estimates: rho = 0.9922299:
    O coeficiente de correlação de Spearman observado foi de 0,99, indicando uma relação positiva, extremamente forte, entre presencas e notas. Isso significa que, à medida que o número de presenças aumenta, as notas tendem a aumentar de forma consistente, mesmo que a relação não seja perfeitamente linear.

Resumo:
Os resultados demonstram uma associação positiva e muito forte entre presenças e notas, estatisticamente significativa. Isso sugere que alunos com mais presenças tendem a obter notas mais altas, mesmo considerando possíveis variações não lineares na relação entre as variáveis.

26.4.3 Kendall

  • H0: \(\tau = 0\) (não há correlação entre as variáveis “x” e “y”)
  • H1: \(\tau \neq 0\) (existe correlação)
cor.test(presencas, notas, method = "kendall")
## 
##  Kendall's rank correlation tau
## 
## data:  presencas and notas
## z = 5.3952, p-value = 6.844e-08
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##       tau 
## 0.9599837

O teste de correlação de Kendall realizado entre as variáveis presencas e notas apresentou os seguintes resultados:

  • z = 5.3952:
    Este é o valor da estatística z calculado para o teste de Kendall. Valores de z elevados indicam forte evidência contra a hipótese nula de ausência de associação entre as variáveis.

  • p-value = 6.844e-08:
    O valor-p extremamente baixo indica que a probabilidade de obter uma correlação tão alta por acaso é praticamente nula. Portanto, a associação observada entre as variáveis é estatisticamente significativa.

  • alternative hypothesis: true tau is not equal to 0:
    A hipótese alternativa do teste é de que o coeficiente de Kendall (\(\tau\)) é diferente de zero, ou seja, existe uma associação monotônica entre as variáveis.

  • sample estimates: tau = 0.9599837:
    O coeficiente de correlação de Kendall (\(\tau\)) encontrado foi de 0,96, indicando uma associação positiva, muito forte, entre presencas e notas. Isso significa que, à medida que o número de presenças aumenta, as notas também tendem a aumentar de forma consistente, mesmo considerando possíveis empates (valores iguais) entre as observações.

Resumo:
Os resultados mostram uma associação positiva e extremamente forte entre presenças e notas, estatisticamente significativa. Isso sugere que alunos com mais presenças tendem a obter notas mais altas, mesmo considerando a ordem dos dados e possíveis empates nas avaliações.

26.5 Tamanho do Efeito (Effect Size)

Em estudos de correlação, o tamanho do efeito é representado pelo valor absoluto do coeficiente de correlação (por exemplo, Pearson, Spearman ou Kendall). Isso significa que consideramos apenas a intensidade da relação entre as variáveis, independentemente de ser positiva ou negativa.

Por exemplo, tanto um coeficiente de +0,65 quanto de -0,65 indicam um tamanho de efeito de 0,65. Quanto mais próximo de 1 (ou -1), mais forte é a correlação; quanto mais próximo de 0, mais fraca.

26.6 Cálculo do Tamanho da Amostra e Poder Estatístico

26.6.1 Exemplo com pwr

Calcular o tamanho da amostra necessário para detectar uma correlação de 0,4 com poder de 80% e α = 0,05:

library(pwr)
pwr.r.test(r = 0.4, power = 0.8, sig.level = 0.05, alternative = "two.sided")
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 45.91614
##               r = 0.4
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided

26.6.2 Verificar o poder para uma amostra de tamanho 30:

pwr.r.test(n = 30, r = 0.4, sig.level = 0.05, alternative = "two.sided")
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 30
##               r = 0.4
##       sig.level = 0.05
##           power = 0.6075135
##     alternative = two.sided

26.7 Outros recursos

Para explorar um pouco mais o estudo de correlação, vamos usar o banco de dados iris, que já vem instalado por padrão no R.

O dataset iris é um conjunto de dados clássico em estatística e aprendizado de máquina (machine learning). Ele contém 150 observações de flores de íris de três espécies diferentes: setosa, versicolor e virginica. As variáveis numéricas são:

  • Sepal.Length: comprimento da sépala (em centímetros), a sépala é a parte externa da flor, que protege os botões florais.

  • Sepal.Width: largura da sépala (em centímetros).

  • Petal.Length: comprimento da pétala (em centímetros), as pétalas são as partes geralmente coloridas da flor.

  • Petal.Width: largura da pétala (em centímetros).

Estas medidas são úteis para estudar relações entre características morfológicas das flores.

26.7.1 Visualização com pairs()

A função pairs() mostra uma matriz de gráficos de dispersão, útil para observar visualmente correlações entre todas as variáveis numéricas.

pairs(iris[, 1:4])

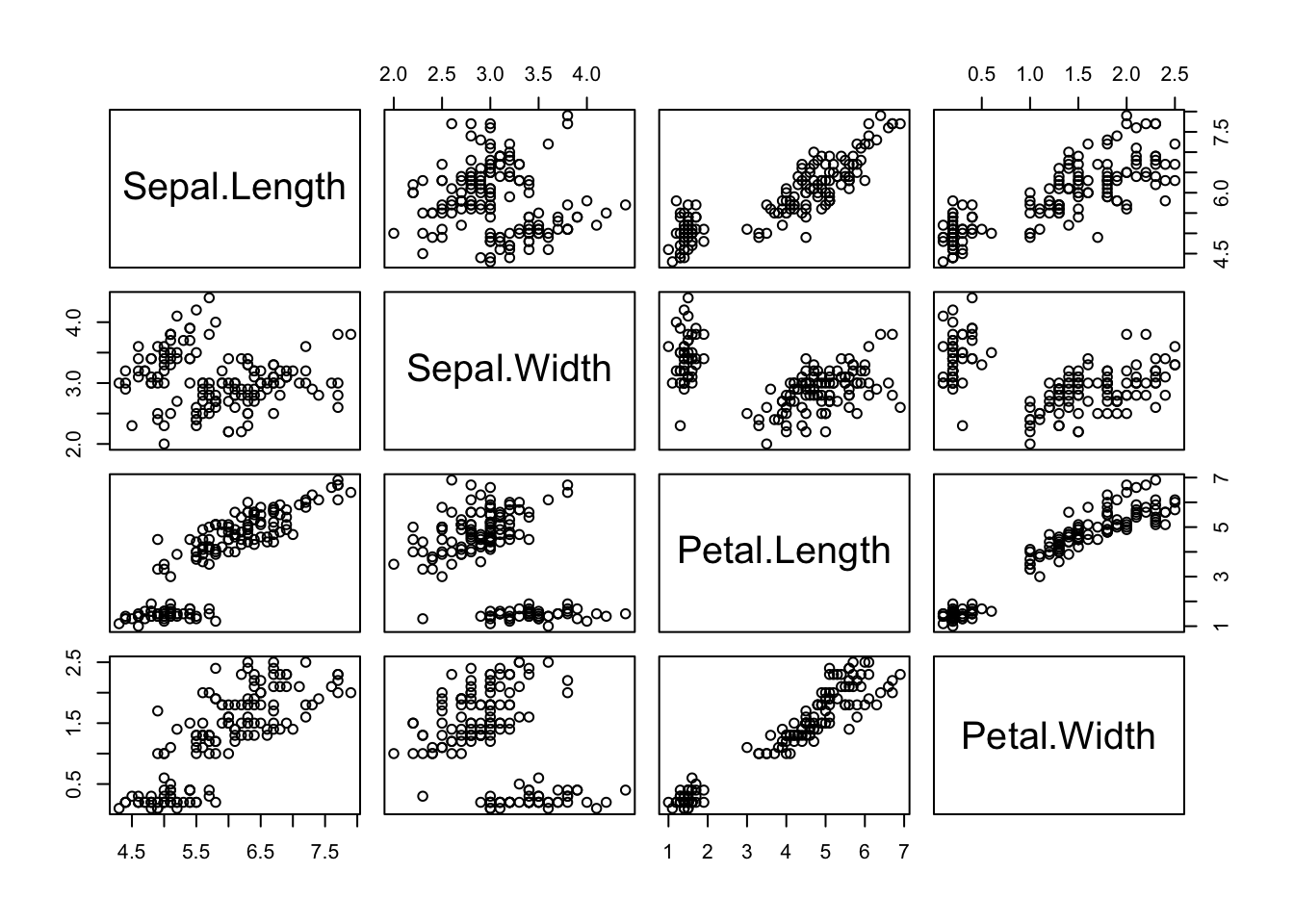
A função pairs no R gera uma matriz de gráficos de dispersão mostrando a relação entre todas as variáveis numéricas de um conjunto de dados. Cada gráfico da matriz compara duas variáveis diferentes:

  • Cada linha e cada coluna representam uma variável.
  • Os gráficos mostram como cada variável se relaciona com as outras: por exemplo, a relação entre Sepal.Length e Petal.Length.
  • Quando os pontos formam uma linha inclinada, isso indica uma correlação (positiva ou negativa) entre as variáveis.
  • Se os pontos estão espalhados, sem padrão, indica pouca ou nenhuma relação.
  • A diagonal mostra o nome de cada variável.

Assim, ao olhar para a matriz, você consegue visualizar rapidamente quais variáveis têm relação entre si e qual é o tipo dessa relação (mais forte, mais fraca, positiva ou negativa).

26.7.2 Matriz de Correlação com cor()

A função cor() calcula a matriz de correlação entre variáveis numéricas. A seguir, uma matriz com correlação de Pearson:

# use o método adequado method = "pearson";  method = "spearman" ou method = "kendall"
cor(iris[, 1:4], method = "pearson")
##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    1.0000000  -0.1175698    0.8717538   0.8179411
## Sepal.Width    -0.1175698   1.0000000   -0.4284401  -0.3661259
## Petal.Length    0.8717538  -0.4284401    1.0000000   0.9628654
## Petal.Width     0.8179411  -0.3661259    0.9628654   1.0000000

A matriz de correlação é uma tabela que mostra os coeficientes de correlação entre todas as combinações possíveis de variáveis numéricas em um conjunto de dados. Cada valor da matriz indica o grau de associação linear entre um par de variáveis. A diagonal principal sempre apresenta o valor 1, pois cada variável é perfeitamente correlacionada com ela mesma. Assim, a matriz de correlação permite identificar rapidamente quais variáveis estão mais relacionadas entre si, facilitando a análise exploratória dos dados. Observe que essa matriz é simétrica

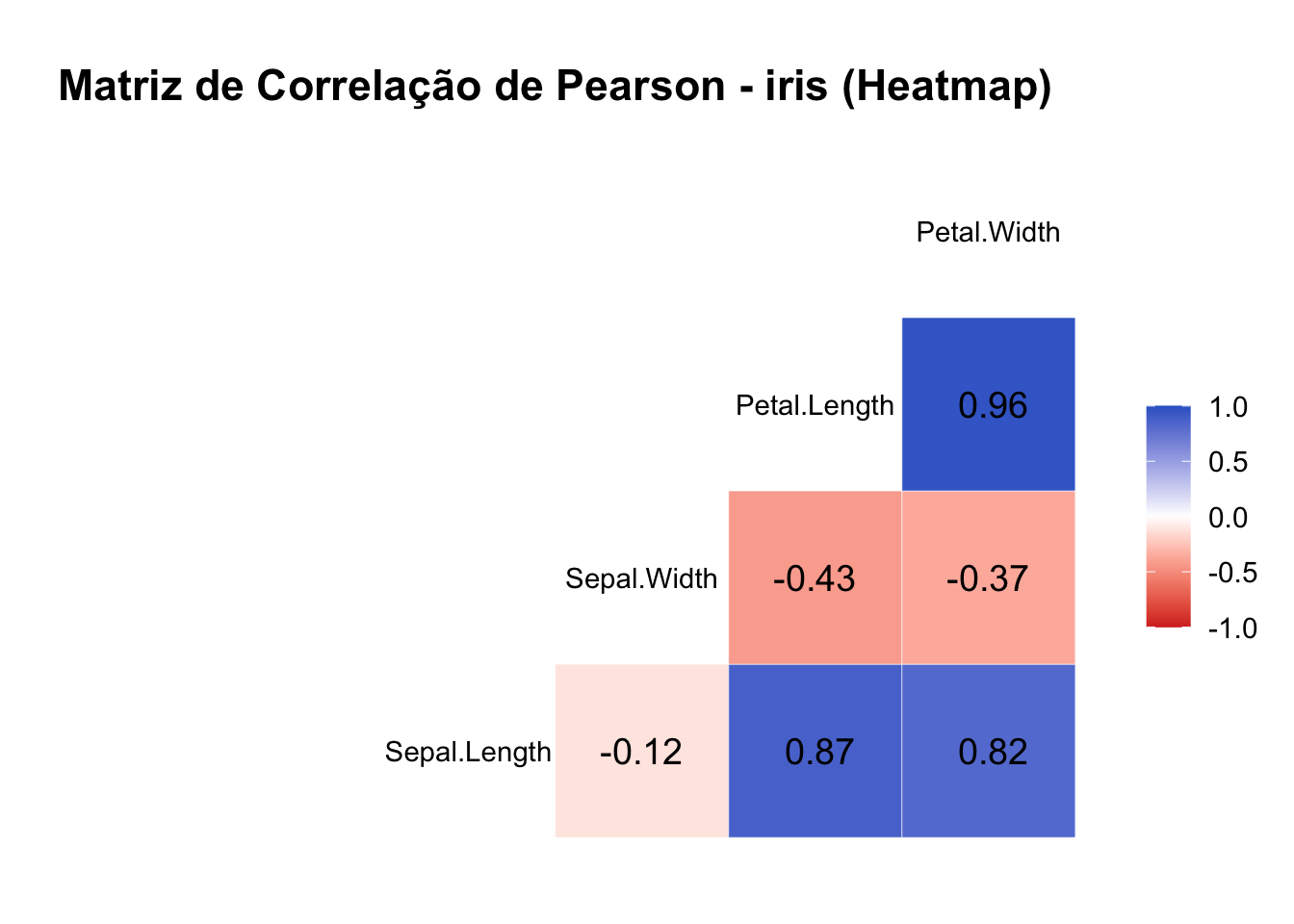
26.7.3 Matriz Visual com GGally::ggcorr()

O ggcorr() do pacote GGally mostra graficamente os coeficientes de correlação, com intensidade e direção representadas por cor.

# Instale os pacotes se necessário:
# install.packages("GGally")
# install.packages("ggplot2")

# Matriz de correlação tipo heatmap com valores destacados
ggcorr(
  data = iris[, 1:4],
  method = c("everything", "pearson"), # calcula todas as correlações de Pearson
  label = TRUE,             # mostra os coeficientes nas células
  label_round = 2,          # arredonda os valores para 2 casas decimais
  label_size = 5,           # tamanho do texto dos coeficientes
  hjust = 0.5,              # centraliza os rótulos nas células
  layout.exp = 2,           # expande o tamanho das células
  low = "#D73027",          # cor para correlação negativa forte
  mid = "white",            # cor para correlação nula
  high = "#3366CC"          # cor para correlação positiva forte
) +
  ggtitle("Matriz de Correlação de Pearson - iris (Heatmap)") +
  theme_minimal(base_size = 14) + # visual minimalista e tamanho de fonte maior
  theme(
    plot.title = element_text(hjust = 0.5, face = "bold"), # centraliza e destaca o título
    axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1) # gira rótulos do eixo x para melhor leitura
  )

A função ggpairs() combina histogramas, correlações e gráficos de dispersão em uma visualização integrada.

Este comando cria uma matriz de gráficos que facilita visualizar a distribuição e a relação entre as variáveis numéricas do conjunto. É muito útil para identificar padrões, tendências, outliers e possíveis correlações antes de uma análise estatística mais aprofundada.

  • Considerando todos os dados:
GGally::ggpairs(iris, columns = 1:4)

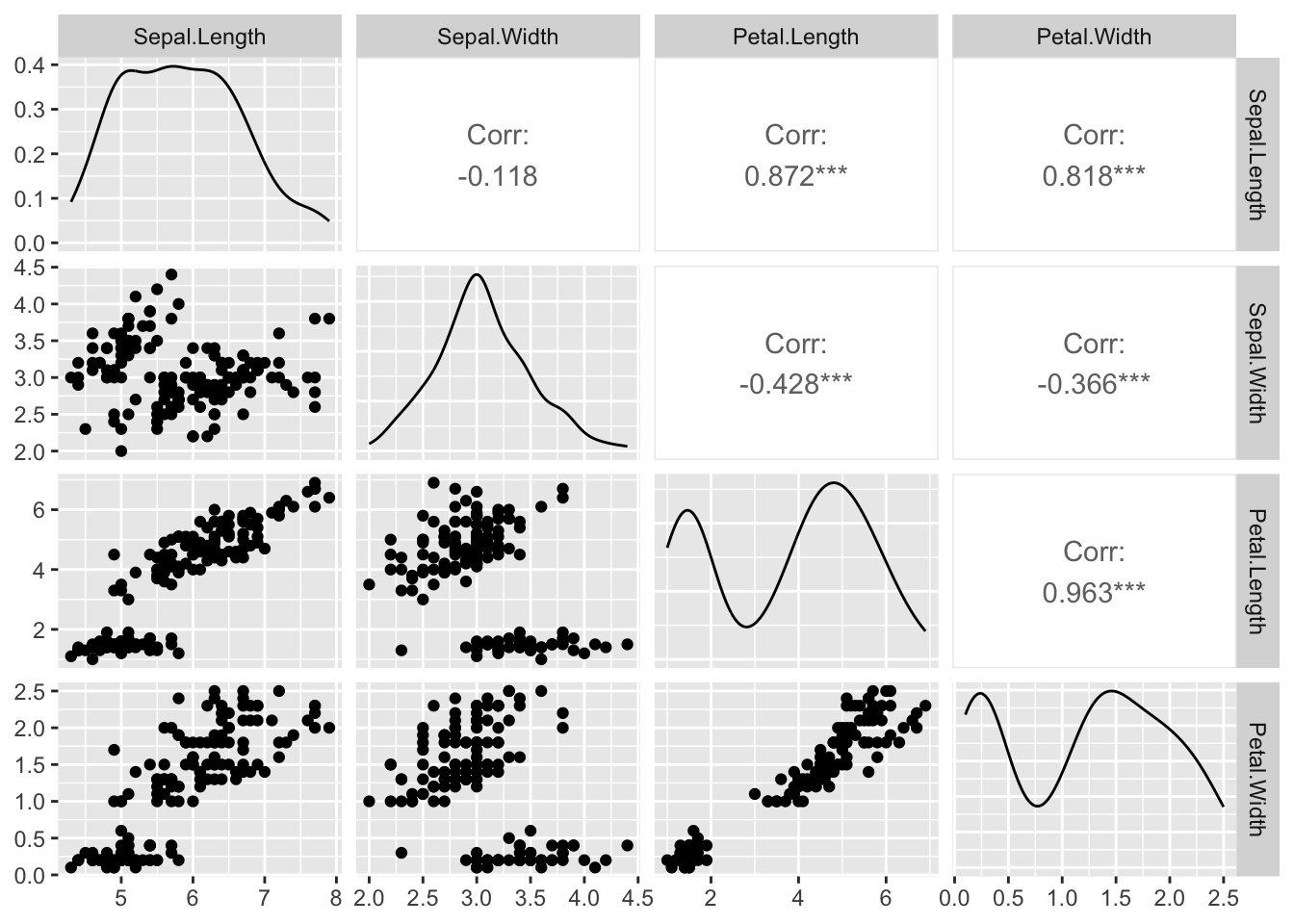
  • Considerando as categorias de especies (variável Species)
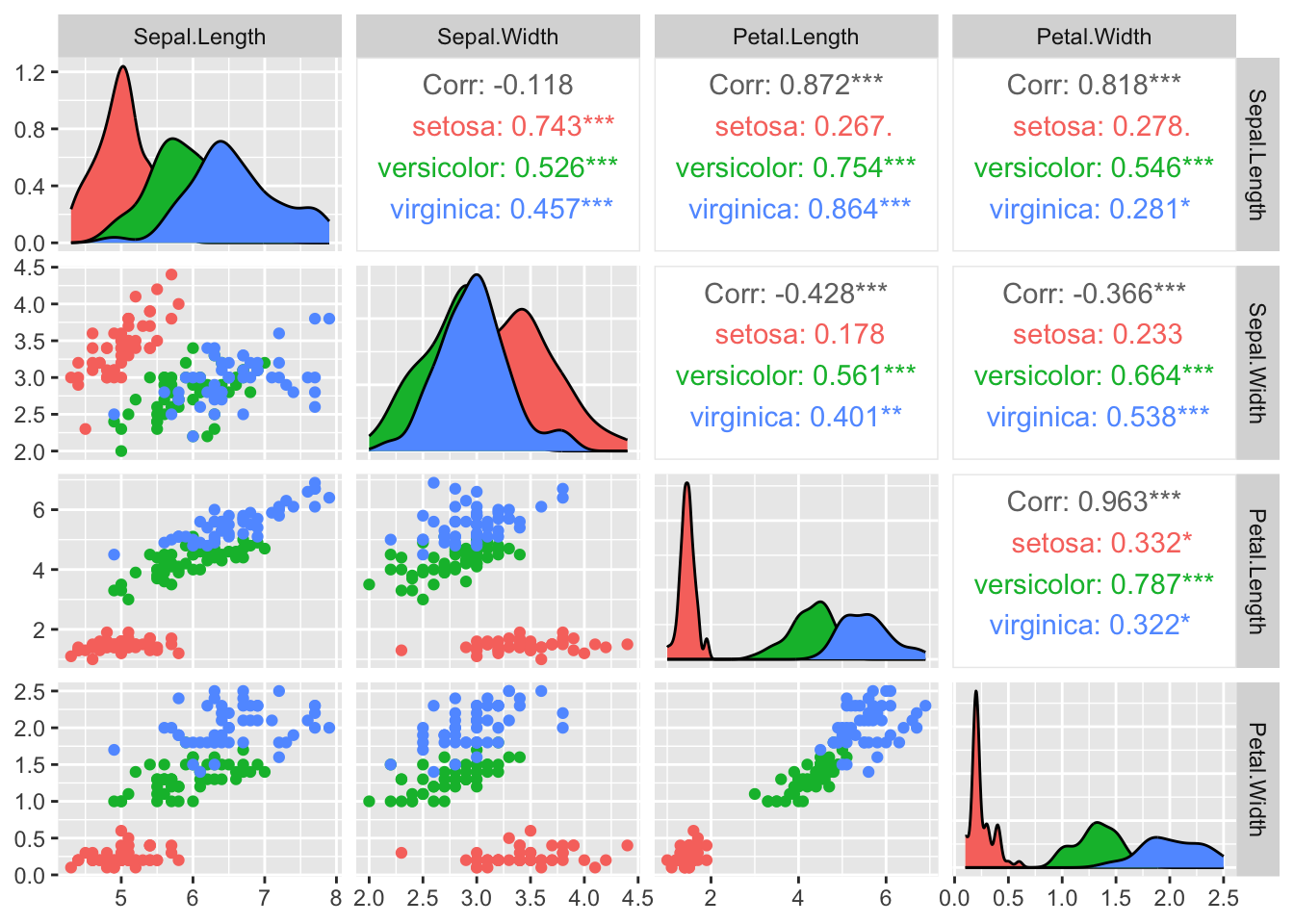
GGally::ggpairs(iris, columns = 1:4, aes(color = Species))

O que a figura mostra?

Esta figura é uma matriz de gráficos de pares (pairs) das variáveis numéricas do conjunto de dados, nesse caso, Sepal.Length, Sepal.Width, Petal.Length e Petal.Width.

  • Diagonal principal: exibe a distribuição de cada variável individualmente, usando histogramas ou curvas de densidade. Quando os dados estão divididos por categoria (como diferentes espécies no exemplo do iris), cada cor representa uma categoria distinta, permitindo visualizar e comparar facilmente como os valores da variável se distribuem em cada grupo.

  • Abaixo da diagonal: mostra gráficos de dispersão, permitindo observar visualmente as relações entre os pares de variáveis para cada espécie.

  • Acima da diagonal: apresenta os coeficientes de correlação para cada par de variáveis:

    • O valor principal (exemplo: Corr: 0.872***) corresponde à correlação considerando todas as espécies juntas.
    • Abaixo, aparecem as correlações por espécie:
      • setosa (vermelho)
      • versicolor (verde)
      • virginica (azul)
    • Os valores são coloridos conforme a espécie correspondente.

  • Sobre os asteriscos: os asteriscos após os valores de correlação indicam o nível de significância estatística do coeficiente calculado, ou seja, quão provável é que a correlação observada seja diferente de zero apenas pelo acaso. A convenção usual é:

  • * : p < 0,05

  • ** : p < 0,01

  • *** : p < 0,001

  • Sem asteriscos: correlação não significativa