Capítulo 4 Tamanho da Amostra

4.1 🎯 Por Que Calcular o Tamanho da Amostra?

O cálculo do tamanho da amostra é uma etapa fundamental no planejamento de qualquer pesquisa científica. Ele determina quantos participantes precisamos incluir no estudo para que os resultados sejam:

  • ✅ Representativos da população estudada
  • ✅ Estatisticamente confiáveis
  • ✅ Precisos o suficiente para responder à pergunta de pesquisa
  • ✅ Viáveis em termos de tempo e recursos

4.1.1 💡 O Que Acontece se Erramos no Tamanho da Amostra?

Amostra Muito Pequena Amostra Muito Grande
❌ Resultados não confiáveis ⚠️ Desperdício de recursos
❌ Conclusões equivocadas ⚠️ Tempo excessivo de coleta
❌ Baixo poder estatístico ⚠️ Custos desnecessários
❌ Pesquisa pode ser invalidada ⚠️ Questões éticas (expor mais pessoas que o necessário)

Em resumo: Calcular corretamente o tamanho da amostra garante que sua pesquisa seja cientificamente válida e eticamente responsável.

4.2 🔢 Tipos de Cálculo Amostral Segundo o Objetivo Estatístico

O método de cálculo amostral varia conforme o que você deseja estimar ou testar:

Objetivo da Pesquisa Tipo de Cálculo Quando Usar Informações Necessárias
Estimar uma proporção Cálculo para proporção Percentual de alunos com ansiedade Margem de erro, nível de confiança, proporção estimada
Estimar uma média Cálculo para média Média de horas de estudo por dia Desvio padrão, margem de erro, nível de confiança
Comparar dois grupos Teste t ou ANOVA Comparar estresse entre cursos Tamanho do efeito, poder estatístico, nível de significância
Testar correlação Cálculo para correlação Relação entre sono e desempenho Tamanho do efeito esperado, poder estatístico
Estudos experimentais Ensaio clínico/experimento Efeito de uma intervenção Grupos controle/experimental, poder, efeito esperado

💭 Importante: Cada tipo de análise estatística requer uma fórmula específica para cálculo amostral!

4.3 📊 Cálculo Para Estimar uma Proporção: Passo a Passo

Quando o objetivo é estimar uma proporção (por exemplo, “Qual percentual de estudantes tem ansiedade?”), precisamos de algumas informações:

4.3.1 🔑 Informações Necessárias

Parâmetro O que é? Exemplo UFTM
1. Tamanho da População (N) Total de indivíduos que você quer estudar 6.900 estudantes
2. Margem de Erro (E) Quanto você aceita “errar” na estimativa 5% (0,05)
3. Nível de Confiança Quão confiante você quer estar 95% (padrão)
4. Proporção Estimada (p) Estimativa inicial do fenômeno 50% (0,5) = pior cenário

4.3.2 📐 A Fórmula

Para população infinita ou muito grande:

\[ n = \frac{Z^2 \cdot p \cdot (1 - p)}{E^2} \]

Onde:

  • \(n\) = tamanho da amostra necessário

  • \(Z\) = valor da distribuição normal padrão

    • Para 95% de confiança: Z = 1,96

    • Para 99% de confiança: Z = 2,58

  • \(p\) = proporção estimada (use 0,5 quando não souber)

  • \(E\) = margem de erro (em decimal: 5% = 0,05)

4.3.3 🧮 Exemplo Prático: Pesquisa na UFTM

Situação: Queremos estimar a proporção de estudantes com sintomas de ansiedade.

Dados:

  • População: 6.900 estudantes

  • Margem de erro: 5% (queremos estar “corretos” com ±5%)

  • Nível de confiança: 95%

  • Proporção estimada: 50% (não sabemos, então usamos o pior cenário)

Cálculo:

\[ n = \frac{1,96^2 \cdot 0,5 \cdot (1 - 0,5)}{0,05^2} \]

\[ n = \frac{3,8416 \cdot 0,5 \cdot 0,5}{0,0025} \]

\[ n = \frac{0,9604}{0,0025} = 384,16 \]

Resultado: Precisamos de 384 estudantes na amostra.

4.3.4 🔄 Ajuste Para População Finita

Quando a população é “pequena” (geralmente N < 10.000), aplicamos uma correção:

\[ n_{ajustado} = \frac{n}{1 + \frac{n-1}{N}} \]

Para nosso exemplo:

\[ n_{ajustado} = \frac{384}{1 + \frac{384-1}{6900}} = \frac{384}{1 + 0,0555} = \frac{384}{1,0555} = 364 \]

Resultado final: Com a correção, precisamos de 364 estudantes.

4.3.5 💭 Interpretando os Resultados

Com uma amostra de 364 estudantes:

✅ Temos 95% de confiança nos resultados
✅ Nossa margem de erro é de ±5%
✅ Os resultados representam bem toda a população (6.900 alunos)

Exemplo prático:
Se 60% da amostra relata ansiedade, podemos dizer que:
"Entre 55% e 65% de TODOS os estudantes da UFTM têm ansiedade"
(com 95% de confiança)

4.4 ⚠️ Atenção: Diferentes Objetivos = Diferentes Cálculos!

Até agora, calculamos amostra apenas para estimar proporção (exemplo: “Qual % de alunos tem ansiedade?”).

Mas o cálculo muda conforme seu objetivo. Veja:

4.4.1 🎯 Tipos de Cálculo Amostral

Seu Objetivo Quando Usar Exemplo Prático O Que Muda no Cálculo
Estimar PROPORÇÃO Quer saber quantos % “Qual % pratica exercícios?” Usa margem de erro e proporção estimada
Estimar MÉDIA Quer saber valor médio “Quantas horas de sono em média?” Precisa do desvio padrão (variabilidade)
Comparar GRUPOS Quer ver se há diferença “Medicina tem mais estresse que Ed. Física?” Precisa do tamanho do efeito esperado
Testar CORRELAÇÃO Quer ver se há relação “Sono afeta o desempenho?” Precisa da força da correlação esperada

4.5 🤔 E Quando Tenho VÁRIOS Objetivos?

4.5.1 Regra Simples:

Calcule CADA objetivo separadamente e use a MAIOR amostra!

4.5.2 Exemplo Prático:

Sua pesquisa tem 4 objetivos:

✓ Estimar % com ansiedade        → precisa de 364 alunos
✓ Calcular média de bem-estar    → precisa de 280 alunos  
✓ Comparar 3 cursos              → precisa de 120 alunos
✓ Testar correlação sono×stress  → precisa de 85 alunos

DECISÃO: Use 364 alunos (o maior número)

Por quê? Porque 364 alunos são suficientes para todos os objetivos!

4.5.3 💡 Dica Extra: Ajuste para Perdas

Nem todos vão participar ou responder. Adicione uma margem de segurança:

Amostra final = Amostra calculada / (1 - % de perda esperada)

Exemplo:
364 / (1 - 0,20) = 364 / 0,80 = 455 alunos

Alcance 455 amostras para garantir 364 respostas válidas

4.6 🛠️ Ferramentas Para Cálculo de Amostra

Nosso foco aqui não é fazer cálculos manualmente, mas sim compreender os conceitos e saber onde buscar ajuda.

Hoje existem ferramentas gratuitas que fazem todo o trabalho para você!

4.6.1 💻 Calculadoras Online (Gratuitas)

Ferramenta Melhor Para Vantagens Link
Calculadora USP Bauru Proporções e médias simples ✅ Rápida e intuitiva
✅ Em português
✅ Não precisa instalar		 Acessar
OpenEpi Estudos em saúde e epidemiologia ✅ Diversos tipos de cálculo
✅ Estudos caso-controle, coorte
✅ Interface simples		 Acessar
G*Power Comparações e testes complexos ✅ Muito completo
✅ Padrão em pesquisas
✅ Calcula poder estatístico		 Download

4.6.2 📊 No Software R (Para Quem Já Usa)

A ideia aqui é simples: em vez de calcular manualmente usando fórmulas matemáticas, usamos funções prontas que fazem tudo para nós!

4.6.2.1 Pacote samplingbook - Cálculo de Amostra para Proporção

# Instalar o pacote (se ainda não tiver)
# install.packages("samplingbook")

# Carregar
library(samplingbook)

# Calcular amostra para proporção (considerando a população infinita)
sample.size.prop(
  e = 0.05,          # Margem de erro (5%)
  P = 0.5,           # Proporção estimada (50%)
  N = Inf,           # Tamanho da população: infinita
  level = 0.95       # Nível de confiança (95%)
  )
## 
## sample.size.prop object: Sample size for proportion estimate
## Without finite population correction: N=Inf, precision e=0.05 and expected proportion P=0.5
## 
## Sample size needed: 385
# Calcular amostra para proporção (considerando a população finita)
sample.size.prop(
  e = 0.05, 
  P = 0.5, 
  N = 6900,           # Tamanho da população: finita 
  level = 0.95
  )
## 
## sample.size.prop object: Sample size for proportion estimate
## With finite population correction: N=6900, precision e=0.05 and expected proportion P=0.5
## 
## Sample size needed: 364

Pronto! Você precisa de 364 estudantes

(Sample = amostra; size = tamanho; needed = necessário → tamanho de amostra necessário)

4.6.2.2 Alternativa: Fórmula Direto no R

# Cálculo direto
N <- 6900
Z <- 1.96
p <- 0.5
E <- 0.05

n <- (Z^2 * p * (1-p)) / E^2
n_final <- ceiling(n / (1 + (n-1) / N))
n_final
## [1] 364

4.6.2.3 ✅ Vantagens

  • ⚡ Rápido e sem erros
  • 📝 Reprodutível (qualquer um pode rodar)
  • 🔄 Fácil testar diferentes cenários

4.6.3 🤖 Usando Inteligência Artificial

Você também pode pedir ajuda a ChatGPT, Copilot ou outras IAs!

💬 Exemplo de prompt:

"Preciso calcular o tamanho da amostra para uma pesquisa 
com estudantes universitários (população de 6.900). 
Quero estimar a proporção de alunos com ansiedade, 
com 95% de confiança e margem de erro de 5%. 
Como faço e qual o resultado?"

⚠️ Importante: Sempre valide os resultados da IA usando uma das calculadoras acima!

4.6.4 🎯 Qual Ferramenta Escolher?

Você é iniciante?
    → Calculadora USP Bauru

Pesquisa na área da saúde?
    → OpenEpi

Precisa comparar grupos ou correlações?
    → G*Power

Já usa R para análises?
    → Pacote pwr, samplingbook

Quer entender o conceito rapidamente?
    → IA + validação em calculadora

4.6.5 💡 Dica Prática

Não sabe qual usar? Faça o seguinte:

1️⃣ Use uma IA para entender o cálculo
2️⃣ Valide em uma calculadora online
3️⃣ Documente qual ferramenta usou no seu projeto

Exemplo de como citar:

“O tamanho amostral foi calculado utilizando a Calculadora Amostral da USP Bauru (http://estatistica.bauru.usp.br/calculoamostral/), considerando população de 6.900 estudantes, margem de erro de 5% e nível de confiança de 95%.”

4.7 🎓 Conclusão

O cálculo do tamanho da amostra é essencial para garantir pesquisas precisas e confiáveis.

A boa notícia? Você não precisa ser expert em matemática!

Com as ferramentas certas, esse processo se torna simples e rápido, permitindo que você foque no que realmente importa: planejar e executar uma pesquisa de qualidade.

4.8 📝 Atividade 2: Análise Crítica do Artigo

Com base no artigo que você buscou na Atividade 1, responda:

4.8.1 🔍 Análise Metodológica

1. Os autores discutem o cálculo do tamanho da amostra?

Investigue:

  • ✅ Há explicação sobre como o tamanho foi determinado?

  • ✅ Mencionam fórmula, software ou ferramenta utilizada?

  • ✅ Apresentam os parâmetros (margem de erro, confiança)?

💭 Se não houver essa informação, isso é uma limitação do estudo?

2. A população da pesquisa foi claramente definida?

Verifique:

  • 👥 Quem compõe a população-alvo?

  • 📋 Há critérios de inclusão e exclusão?

  • 🌍 O contexto está bem delimitado (local, período)?

💭 Uma população mal definida compromete a validade dos resultados.

3. O tamanho da amostra utilizado foi adequado?

Avalie criticamente:

  • ✅ A amostra parece grande o suficiente?

  • ⚖️ É representativa da população?

  • ⚠️ Os autores discutem limitações relacionadas ao tamanho da amostra?

4.8.2 🧮 Cálculo Prático

4. Refaça o cálculo do tamanho de amostra

Use uma das ferramentas indicadas e preencha:

Item Informação do Artigo Seu Cálculo
Tamanho da população (N)
Margem de erro
Nível de confiança
Tipo de cálculo necessário
Tamanho no artigo
Seu resultado
Coincidem? ☐ Sim ☐ Não

💭 Se não coincidem, quais podem ser as razões?

4.8.3 ⚖️ Aspectos Éticos

5. A pesquisa foi aprovada pelo Comitê de Ética?

Procure no artigo:

  • ✅ Há menção à aprovação do CEP?

  • 📋 O número do parecer está informado?

  • 📝 Há referência ao TCLE (Termo de Consentimento)?

6. Qual a importância de submeter ao Comitê de Ética?

Reflita sobre:

Aspecto Por Que É Importante?
Proteção dos participantes Garante que os direitos sejam respeitados
Consentimento informado Participação voluntária e esclarecida
Confidencialidade Proteção dos dados pessoais
Riscos e benefícios Avaliação ética da relação custo-benefício
Integridade científica Credibilidade da pesquisa

⚠️ Consequências de NÃO submeter:

  • Violação de direitos dos participantes

  • Infração às Resoluções CNS 466/2012 e 510/2016

  • Artigo pode ser rejeitado ou retratado

  • Sanções ao pesquisador

4.8.4 📚 Para Saber Mais

Conheça o Comitê de Ética em Pesquisa (CEP) da UFTM

🔗 https://www.uftm.edu.br/comitesecomissoes/cep

Você encontrará:

  • Como submeter projetos

  • Documentos necessários

  • Prazos e tramitação

  • Regulamentações vigentes

💬 Questão bônus: Se você fosse revisor deste artigo, aprovaria a metodologia amostral? Justifique.

4.9 🧮 Exercício Prático: Calculadora USP Bauru

4.9.1 🎯 Situação-Problema

Você é pesquisador(a) e quer investigar a adesão ao uso de equipamentos de proteção individual (EPIs) entre profissionais de enfermagem de um hospital universitário.

Dados da instituição:

  • População: 450 profissionais de enfermagem (enfermeiros, técnicos e auxiliares)

  • Estimativa inicial: Estudos semelhantes mostram que cerca de 70% dos profissionais utilizam EPIs corretamente

  • Parâmetros desejados: 95% de confiança e margem de erro de 5%

Pergunta: Quantos profissionais você precisa incluir na sua amostra?

4.9.2 📝 Passo a Passo na Calculadora

1. Acesse a calculadora:

2. Preencha os campos conforme a imagem:

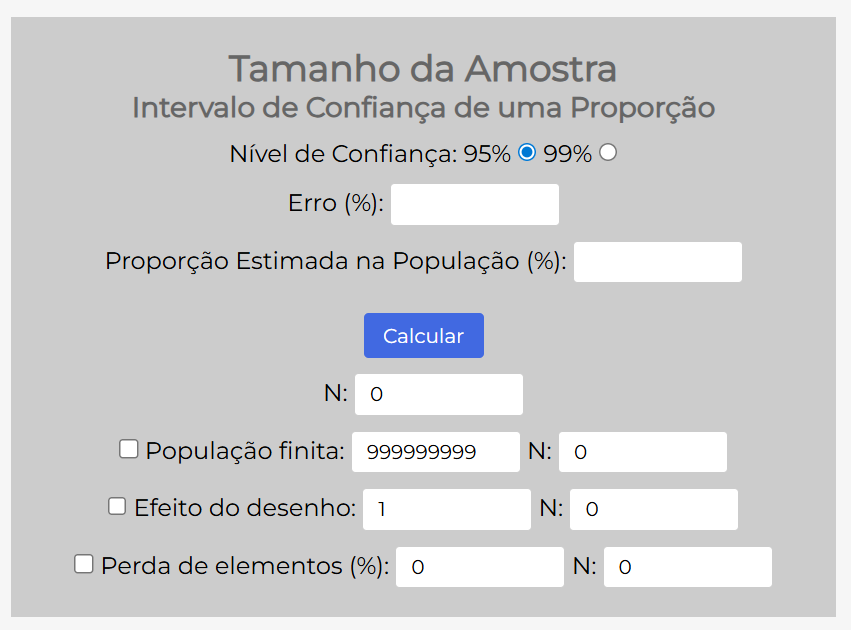
Calculadora USP Bauru
Calculadora USP Bauru
Campo O que colocar Valor
Nível de Confiança Deixe marcado 95% 🔵 95%
Erro (%) Margem de erro desejada 5
Proporção Estimada na População (%) Uso correto de EPIs 70
☑️ População finita ✅ Marque a caixa 450

3. Clique em “Calcular”

4.9.3 ✅ Anote Seus Resultados

a) Quantos profissionais você precisa pesquisar?

R: _______ profissionais

b) Qual a diferença do tamano da amostra considerando população finita e infinita?

R: sem considerar população finita (infinita): _______ profissionais

R: considerando população finita (450): _______ profissionais

Diferença: _______ profissionais

c) Volte às configurações originais. Agora aumente o nível de confiança para 99%. O que acontece?

R: com 99% de confiança: _______ profissionais

d) Retorne para 95% de confiança. Agora diminua a margem de erro para 3%. Qual o impacto?

R: com erro de 3%: _______ profissionais

e) Use o campo “Perda de elementos (%)” e considere 20% de perdas (profissionais de férias, licença, recusa). Quantas amostras você deveria ter?

R: ajustado para perdas: _______ profissionais

4.9.4 🎓 Questões Para Reflexão

1. Viabilidade prática:
Considerando que você precisa pesquisar _____ profissionais de um total de 450, isso representa aproximadamente _____% da população. Isso é viável? Por quê?

2. Comparação:
Por que o tamanho da amostra é MENOR quando consideramos população finita (450) em vez de infinita?

3. Decisões metodológicas:
Se você tivesse que escolher entre:

  • Opção A: Erro 5% e confiança 95%

  • Opção B: Erro 3% e confiança 95%

Qual você escolheria considerando tempo e recursos limitados? Justifique.

4.9.5 💡 Desafio Extra: Mude o Contexto

Agora imagine um cenário diferente:

Situação: Você não tem ideia de qual a proporção de profissionais que usam EPIs corretamente.

O que fazer? Quando não temos estimativa prévia, usamos 50% (pior cenário, que gera maior amostra).

Teste: Volte à calculadora e mude a “Proporção Estimada” para 50%. Recalcule.

Qual o novo tamanho da amostra? _______ profissionais

Por que mudou? _______________________________________

4.9.6 ✅ Gabarito

👁️ Clique para ver as respostas

População finita: 450 profissionais | Proporção: 70%

a) Amostra necessária (erro 5%, conf 95%): 189 profissionais

b) Comparação:

  • Sem população finita (infinita): 323 profissionais

  • Com população finita (450): 189 profissionais

  • Diferença: 134 profissionais (a correção reduz bastante!)

c) Com 99% de confiança:

  • pop. finita: 250 profissionais (aumenta!)

  • pop. infinita: 560 profissionais (nem faz sentido, por ser maior que a população)

d) Com erro de 3%:

  • pop. finita: 300 profissionais (pop finita)

  • pop. infinita: 897 profissionais (nem faz sentido)

e) Ajustado para 20% de perdas:

  • pop. finita: 312 profissionais (250 ÷ 0,80)

Desafio Extra (proporção 50%):

  • pop. finita: 269 profissionais
  • Mudou porque 50% é o cenário mais conservador (gera maior variabilidade)

🤔 Entendendo a Variabilidade

Pense assim: quando calculamos o tamanho da amostra para proporção, usamos a fórmula que inclui p × (1 - p), onde p é a proporção estimada.

Veja o que acontece com diferentes proporções:

Proporção (p) Cálculo p × (1-p) Variabilidade
10% (0,10) 0,10 × 0,90 = 0,09 Baixa
30% (0,30) 0,30 × 0,70 = 0,21 Média
50% (0,50) 0,50 × 0,50 = 0,25 MÁXIMA ✅
70% (0,70) 0,70 × 0,30 = 0,21 Média
90% (0,90) 0,90 × 0,10 = 0,09 Baixa

📊 Observe: O valor 0,25 (quando p = 50%) é o MAIOR POSSÍVEL!

Reflexão 1: 189/450 = 42% da população - é uma amostra grande, mas viável em um hospital.

Reflexão 2: A correção para população finita considera que estamos pegando uma fração significativa do total (42%), então precisamos de menos pessoas para ter precisão.

4.9.7 🎯 O Que Você Aprendeu

✅ Como usar a Calculadora USP Bauru passo a passo
✅ A importância da correção para população finita
✅ Como confiança e erro afetam o tamanho da amostra
✅ Por que usar 50% quando não temos estimativa
✅ Como ajustar para perdas esperadas

💬 Próximo passo: Use esses conhecimentos para calcular a amostra da SUA pesquisa!